详解最大似然估计、最大后验概率估计,以及贝叶斯公式的理解
[TOC]
我们先从概率和统计的区别讲起。
概率和统计的区别
概率(probability)和统计(statistic)看上去是两个相近的概念,其实研究的问题刚刚好相反。
概率研究的问题是,已知数据的模型和参数,怎么预测这个模型产生的结果,包括研究这些结果的特性(均值,方差,协方差等等)。
统计研究的问题则相反。在实际中我们观察或者测试得到一组数据,要利用这组数据去预测模型和参数。找到最好最适合这些数据的模型(高斯分布,泊松分布,指数分布,拉普拉斯分布等等)
一句话总结:概率是已知模型和参数,推数据;统计是已知数据,推模型和参数。
本文中的最大似然估计(MLE)和最大后验估计(MAP)都是统计领域的问题。都是用来推测参数的方法,为什么会有两种不同的方法,我们先来看贝叶斯公式。
贝叶斯公式
贝叶斯定理(英语:Bayes’ theorem)是概率论中的一个定理,描述在已知一些条件下,某事件的发生概率。比如,如果已知某人妈妈得癌症与寿命有关,使用贝叶斯定理则可以通过得知某人年龄,来更加准确地计算出他妈妈罹患癌症的概率。
通常,事件A在事件B已发生的条件下发生的概率,与事件B在事件A已发生的条件下发生的概率是不一样的。然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。贝叶斯公式的一个用途,即透过已知的三个概率而推出第四个概率。贝叶斯定理跟随机变量的条件概率以及边际概率分布有关。
作为一个普遍的原理,贝叶斯定理对于所有概率的解释是有效的。这一定理的主要应用为贝叶斯推断,是推论统计学中的一种推断法。这一定理名称来自于托马斯·贝叶斯。
贝叶斯公式的定义
贝叶斯定理是关于随机事件A和B的条件概率的一则定理。
其中A以及B为随机事件,且P(B)不为零。


在贝叶斯定理中,每个名词都有约定俗成的名称:
是已知
发生后,
的条件概率]。也称作
的后验概率。
是
的先验概率(或边缘概率)。其不考虑任何
方面的因素。
是已知
发生后,
的条件概率。也可称为
的后验概率。某些文献又称其为在特定
时,
的似然性,因为
。
是
的先验概率。
按这些术语,贝叶斯定理可表述为:
后验概率 = (似然性*先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
| 另外,比例也有时被称作标准似然度(standardised likelihood),贝叶斯定理可表述为: |
后验概率 = 标准似然度*先验概率
二选一的形式
贝叶斯理论通常可以再写成下面的形式:
|  |
其中$A^C$是A的补集(即非A)。故上式亦可写成:
|  |
在更一般化的情况,假设${A_i}$是事件集合里的部分集合,对于任意的${A_i}$ ,贝叶斯理论可用下式表示:
|  |
贝叶斯公式就是在描述,你有多大把握能相信一件证据?(how much you can trust the evidence) \(P(B|A^{C})P(A^{C})=0\)
似然函数
似然(likelihood)这个词其实和概率(probability)是差不多的意思,Colins字典这么解释:The likelihood of something happening is how likely it is to happen. 你把likelihood换成probability,这解释也读得通。但是在统计里面,似然函数和概率函数却是两个不同的概念(其实也很相近就是了)。
对于这个函数: \(P(x|\theta)\) 输入有两个:x表示某一个具体的数据;θ表示模型的参数。
如果θ是已知确定的,x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点x,其出现概率是多少。
如果x是已知确定的,θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现x这个样本点的概率是多少。
比如, , 即x的y次方。如果x是已知确定的(例如x=2),这就是
, 这是指数函数。 如果y是已知确定的(例如y=2),这就是
,这是二次函数。同一个数学形式,从不同的变量角度观察,可以有不同的名字。
接下来我们来看看MLE和MAP是什么:
最大似然估计(MLE)
假设有一个造币厂生产某种硬币,现在我们拿到了一枚这种硬币,想试试这硬币是不是均匀的。即想知道抛这枚硬币,正反面出现的概率(记为θ)各是多少?
这是一个统计问题,回想一下,解决统计问题需要什么? 数据!
于是我们拿这枚硬币抛了10次,得到的数据(x0 )是:反正正正正反正正正反。我们想求的正面概率θ是模型参数,而抛硬币模型我们可以假设是 二项分布。
那么,出现实验结果x_0(即反正正正正反正正正反)的似然函数是多少呢?
\(f(x_0 ,\theta) = (1-\theta)\times\theta\times\theta\times\theta\times\theta\times(1-\theta)\times\theta\times\theta\times\theta\times(1-\theta) = \theta ^ 7(1 -\theta)^3\) 注意,这是个只关于θ的函数。而最大似然估计,顾名思义,就是要最大化这个函数。我们可以画出f(θ)的图像:
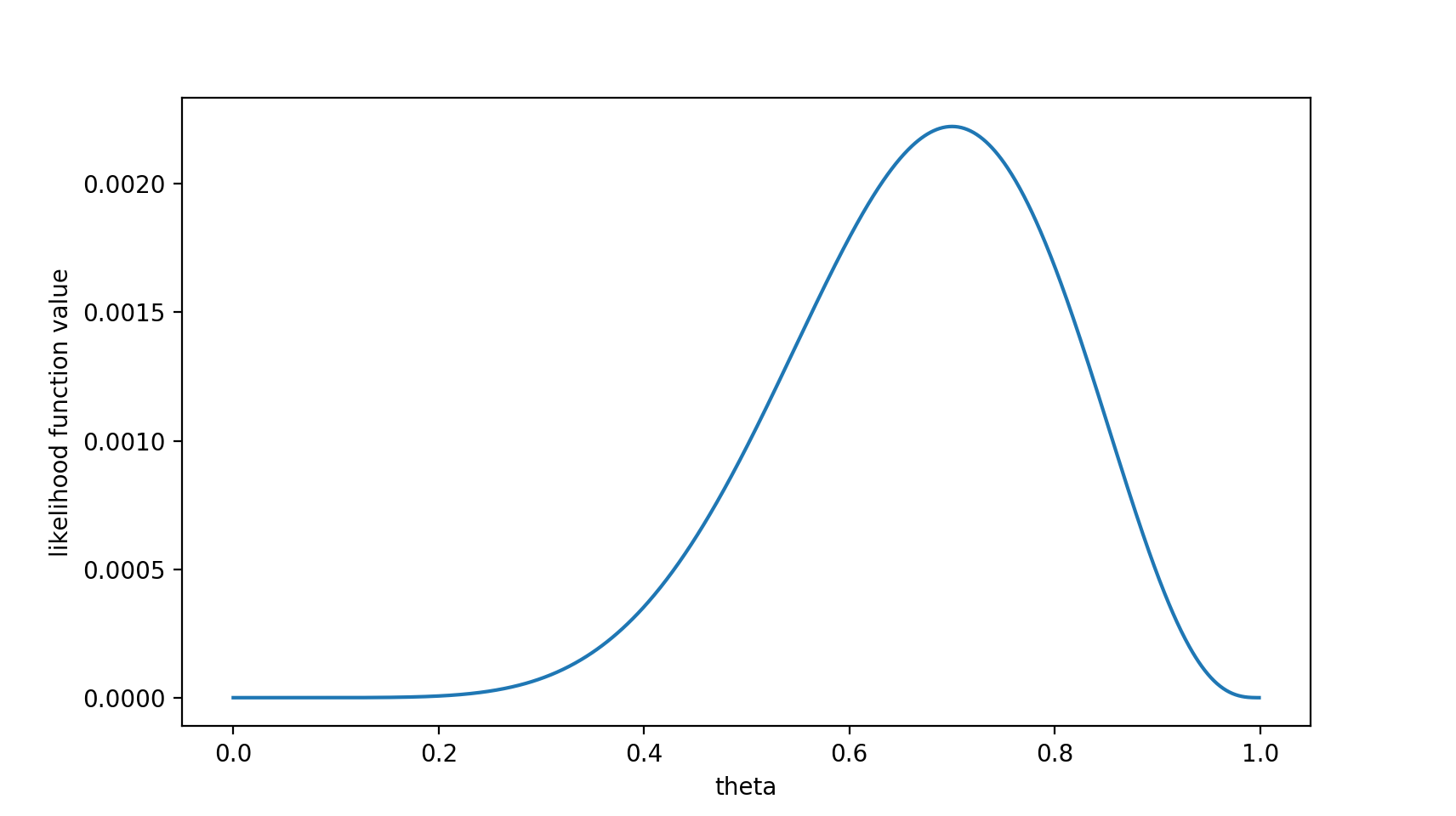
可以看出,在θ=0.7时,似然函数取得最大值。
这样,我们已经完成了对θ的最大似然估计。即,抛10次硬币,发现7次硬币正面向上,最大似然估计认为正面向上的概率是0.7。(ummm…这非常直观合理,对吧?)
且慢,一些人可能会说,硬币一般都是均匀的啊! 就算你做实验发现结果是“反正正正正反正正正反”,我也不信θ=0.7。
这里就包含了贝叶斯学派的思想了——要考虑先验概率。 为此,引入了最大后验概率估计。
为什么在一般定义中会取对数?
如下图所示,一般定义中,极大似然估计我们会对似然函数取对数。

最大后验概率估计
最大后验概率估计 最大似然估计是求参数θ, 使似然函数$ P(x_0|\theta) $最大 。求得的$\theta$不单单让似然函数大,$\theta$自己出现的先验概率也得大。 (这有点像正则化里加惩罚项的思想,不过正则化里是利用加法,而MAP里是利用乘法)
MAP其实是在最大化 \(P(\theta|x_0) = \frac{P(x_0|\theta)P(\theta)}{P(x_0)}\) ,不过因为$x_0$ 是确定的(即投出的“反正正正正反正正正反”),$P ( x_0 )$是一个已知值,所以去掉了分母。(假设“投10次硬币”是一次实验,实验做了1000次,“反正正正正反正正正反”出现了n次,则$P(x_0)=n/1000$。总之,这是一个可以由数据集得到的值)。最大化$P(\theta | x_0)$的意义也很明确,$x_0$已经出现了,要求$ \theta$取什么值使$ P(\theta | x_0)$最大。顺带一提,$ P(\theta | x_0)$即后验概率,这就是“最大后验概率估计”名字的由来。
对于投硬币的例子来看,我们认为(”先验地知道“)
$\theta$取0.5的概率很大,取其他值的概率小一些。我们用一个高斯分布来具体描述我们掌握的这个先验知识,例如假设$P(\theta)$为均值0.5,方差0.1的高斯函数,如下图:
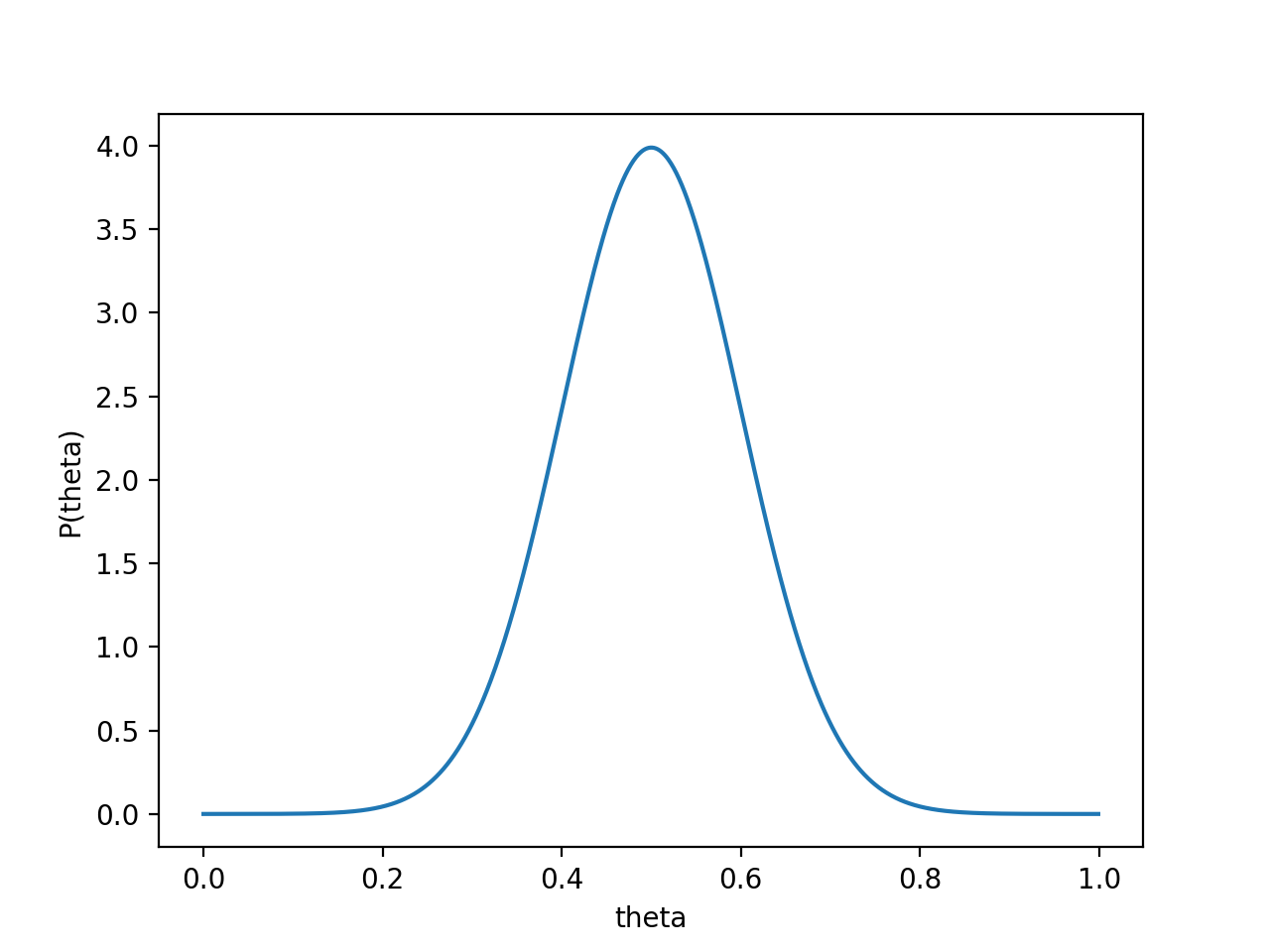
则$P(x_0∣\theta)P(\theta)$的函数为每个事件出现的情况(一般是$P(\theta)$或者是$1-P(\theta)$)和先验函数$P(\theta)$的乘积,图像为:
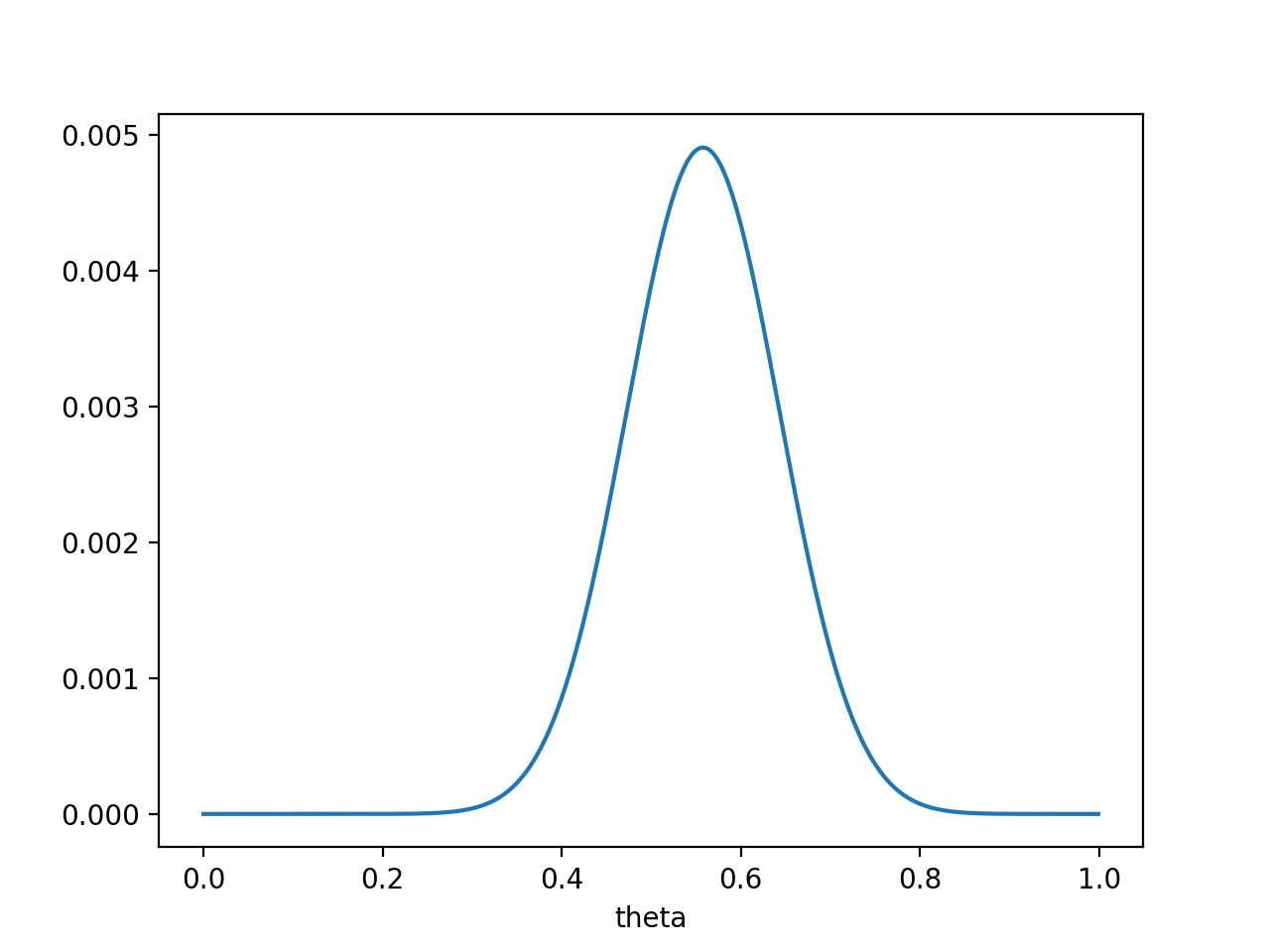
注意,此时函数取最大值时,θ 取值已向左偏移,不再是0.7。实际上,在θ=0.558时函数取得了最大值。即用最大后验概率估计,得到θ=0.558
最后,那要怎样才能说服一个贝叶斯派相信θ=0.7呢?你得多做点实验。
如果做了1000次实验,其中700次都是正面向上,这时似然函数为:
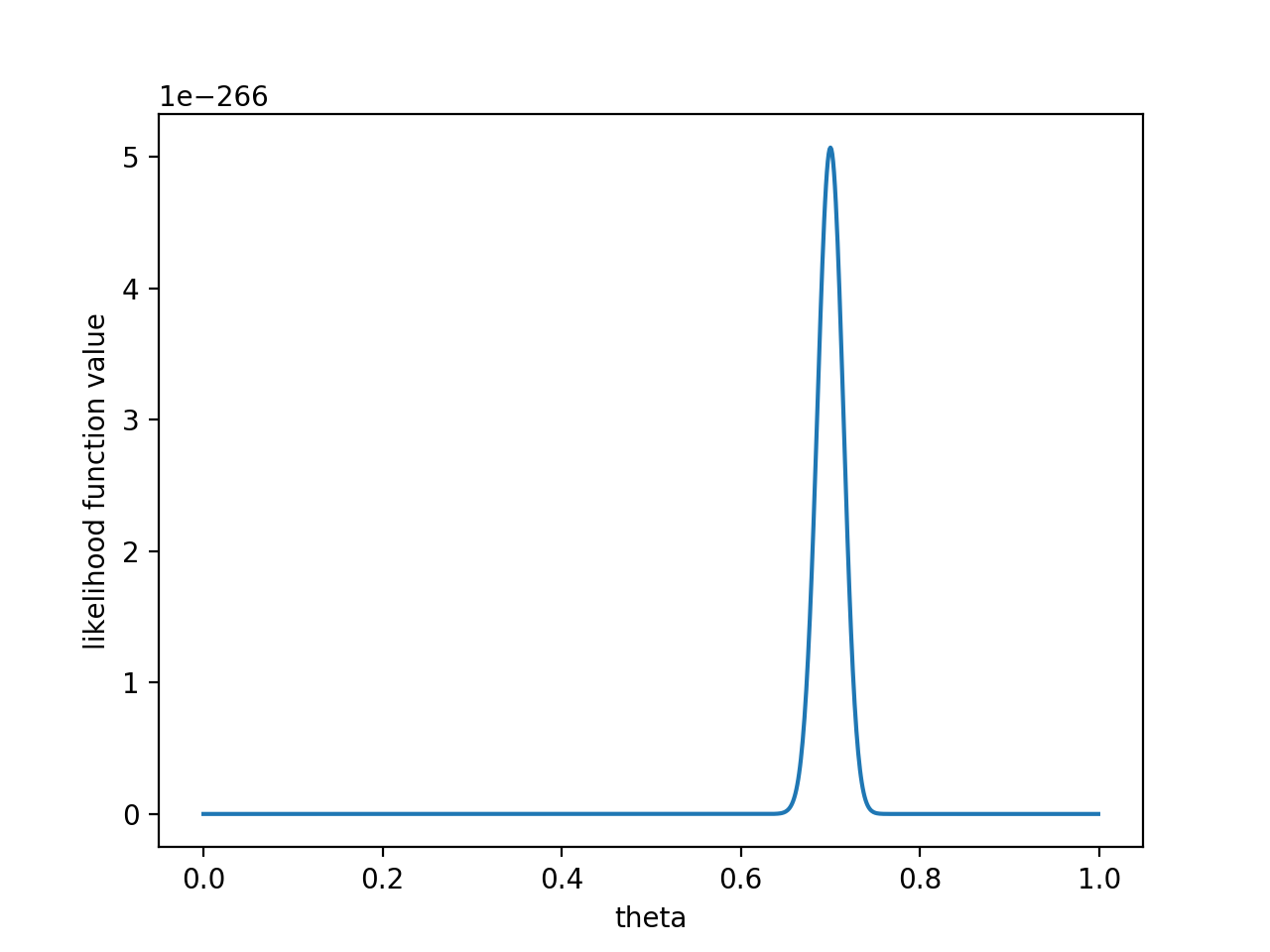
如果仍然假设P(θ)为均值0.5,方差0.1的高斯函数,$P(x_0 ∣θ)P(θ)$的函数图像为:
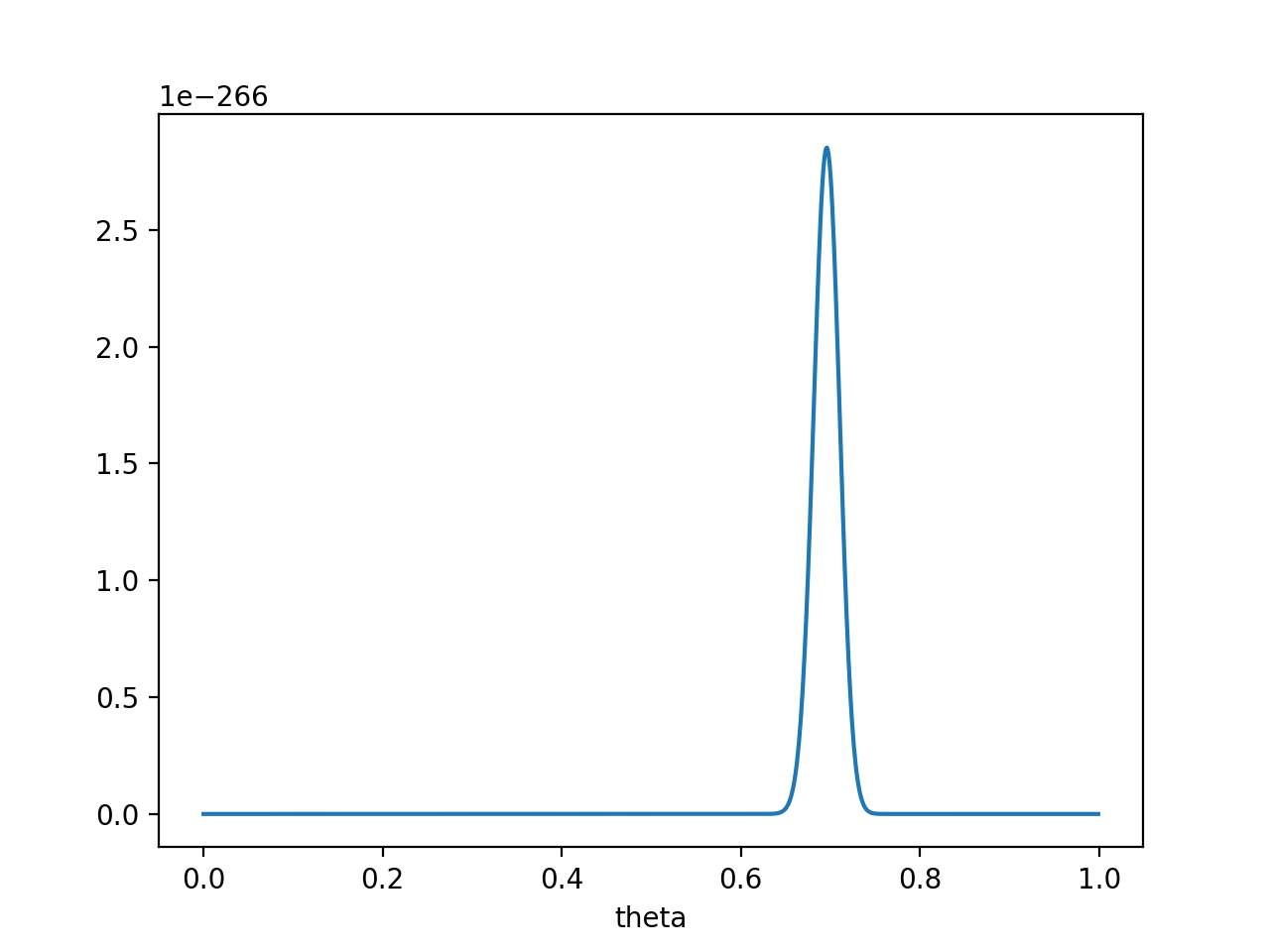
在θ=0.696处,$P(x_0∣θ)P(θ)$取得最大值。
这样,就算一个考虑了先验概率的贝叶斯派,也不得不承认得把θ估计在0.7附近了。
参考
文档信息
- 本文作者:Kilin
- 本文链接:https://star-twinking.github.io/2021/09/04/%E8%AF%A6%E8%A7%A3%E6%9C%80%E5%A4%A7%E4%BC%BC%E7%84%B6%E4%BC%B0%E8%AE%A1-%E6%9C%80%E5%A4%A7%E5%90%8E%E9%AA%8C%E6%A6%82%E7%8E%87%E4%BC%B0%E8%AE%A1-%E4%BB%A5%E5%8F%8A%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%85%AC%E5%BC%8F%E7%9A%84%E7%90%86%E8%A7%A3/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)
