相干成像和非相干成像

相干的定义

首先我们来了解一下什么是相干,引用一下维基百科的定义：

In physics, two wave sources are coherent if their frequency and waveform are identical. Coherence is an ideal property of waves that enables stationary (i.e. temporally and spatially constant) interference.

也就是，两个波之间是否存在关联或者相似程度的一个表示，主要有两个特征，时间相干性(Temporally)和空间相干性(Spatially)。

Spatially coherence:

时间相干性的例子在迈克尔逊干涉仪里面很好地体现了。 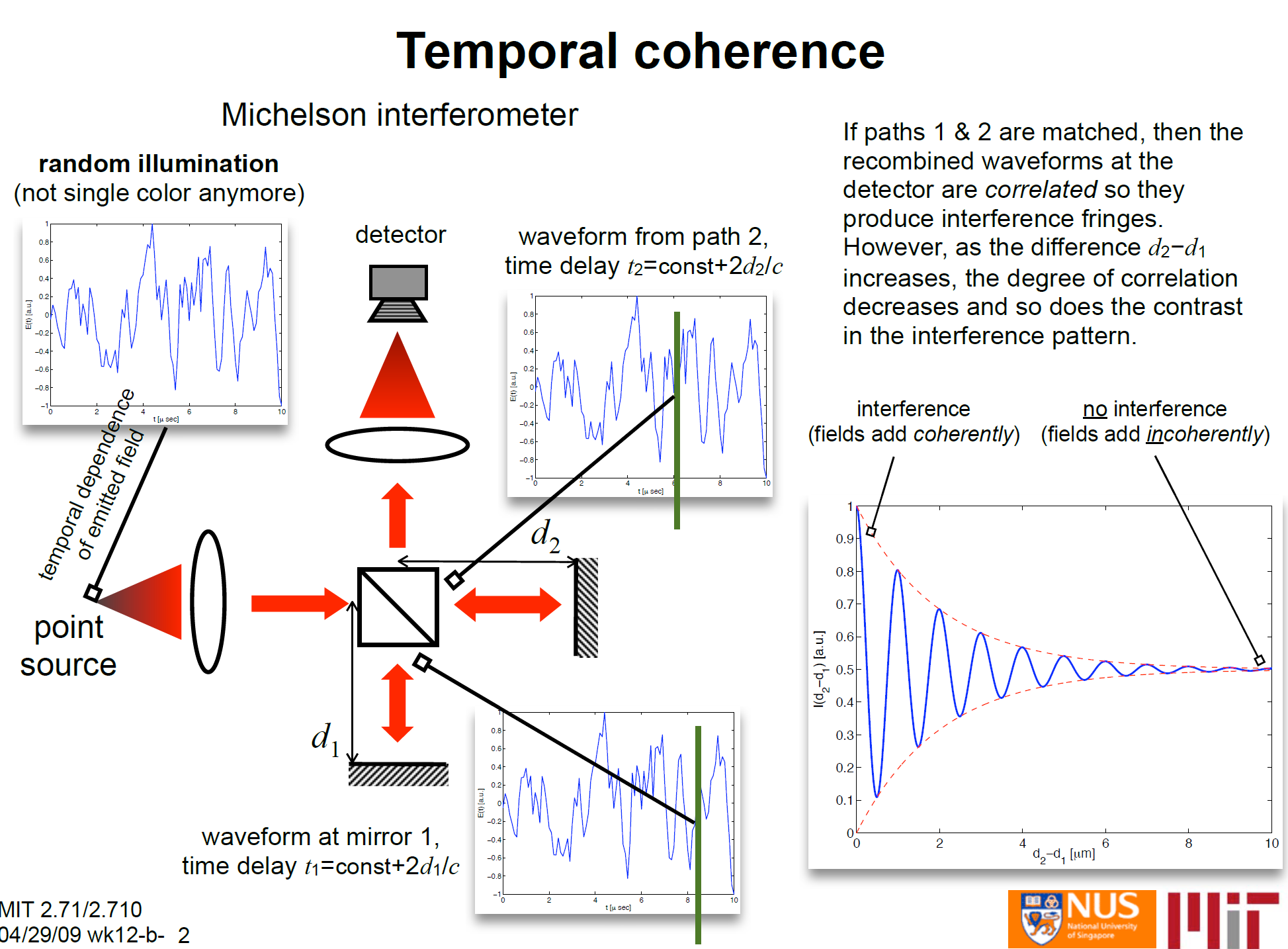d2-d1的时间差就是时间相干性的体现。因为d2-d1越来越大，所以他们之间的时间相干性会越来越小。所以最外层会有一个红色的包络线。

Temporally coherence:

空间相干性则在杨氏双缝干涉里面体现了。

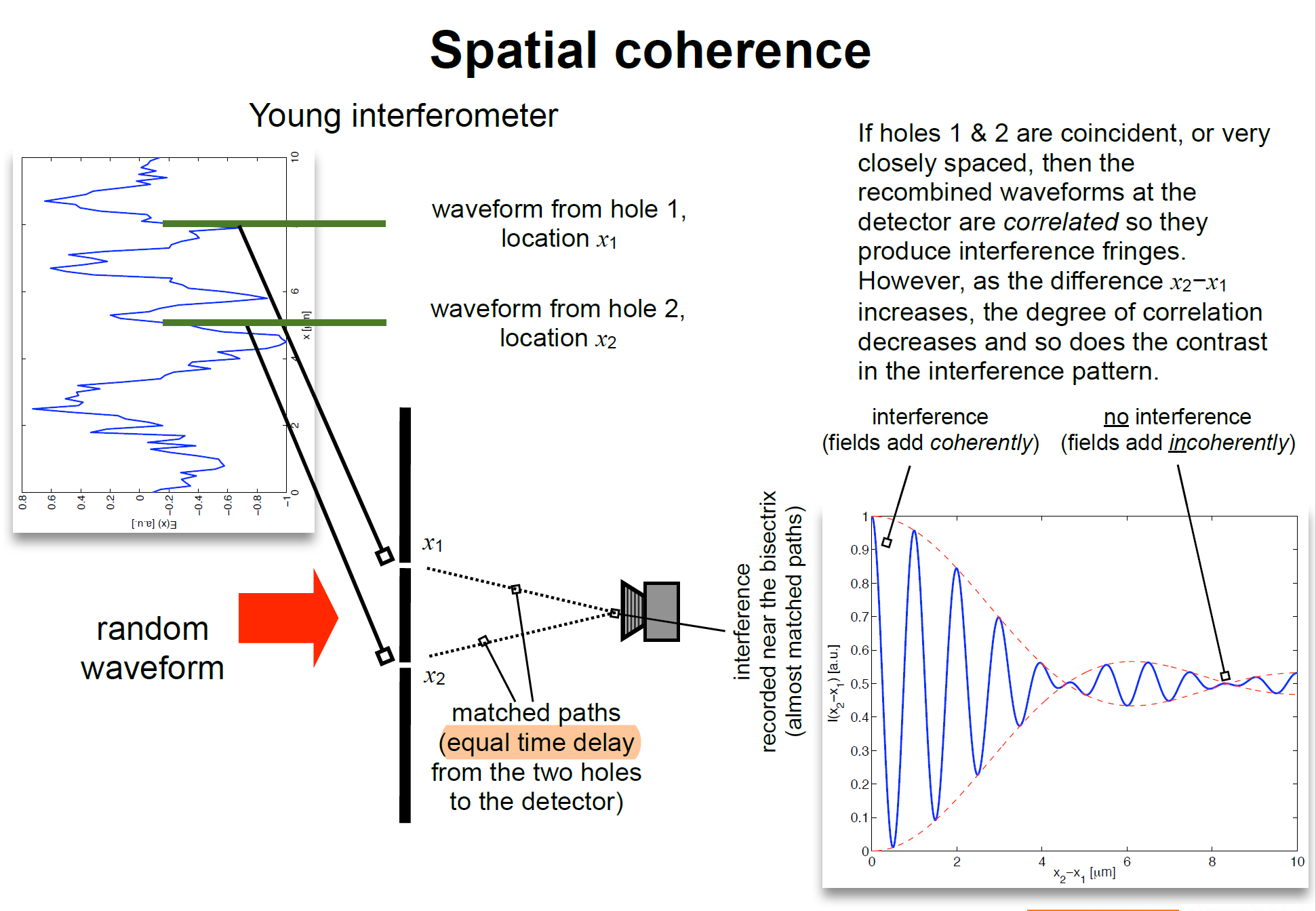
空间相干性可以通过不同干涉条纹的对比度来体现。在中间的对比度最好，因为此时两个的时间差一样，空间上最接近。正常情况下，如果不考虑空间相干性，随着条纹向外移动，两个波的相位叠加在变化，遇到周期为2$\pi$时，又会到最大值。应该是一个没有红色包络线的余弦曲线，但是因为空间上相干性越来越小，所以会在外面有一层包络。

相干叠加和非相干叠加的区别

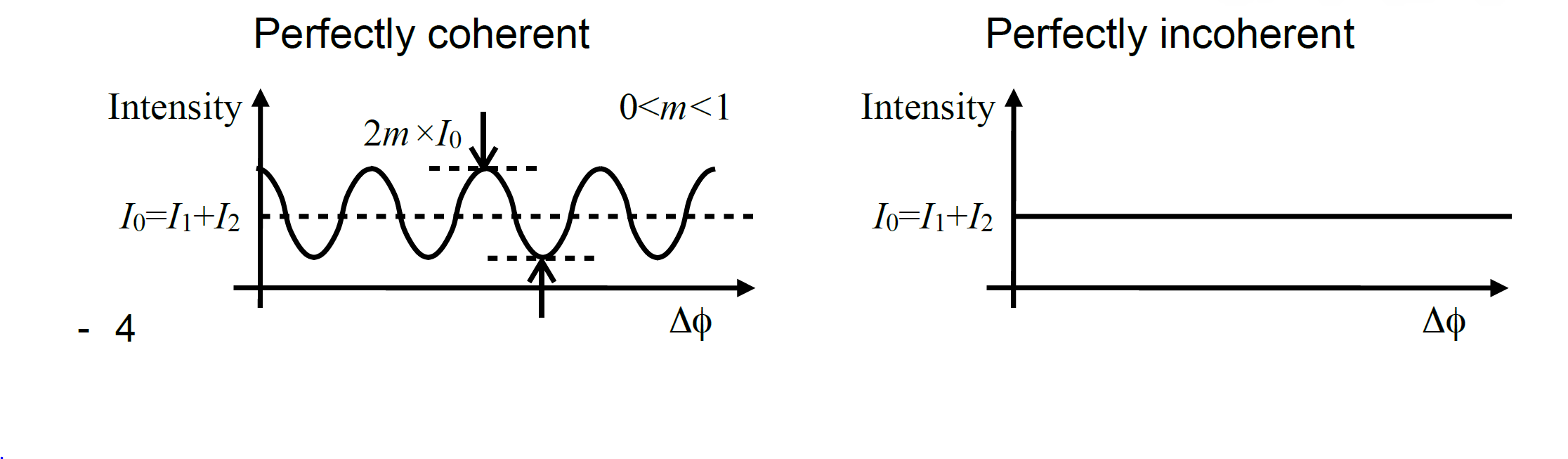
结论：

相干叠加有相位之间的叠加，会随着相位变化波动；非相干叠加是强度叠加，理想非相干情况下，是一个不波动的叠加。

公式上：

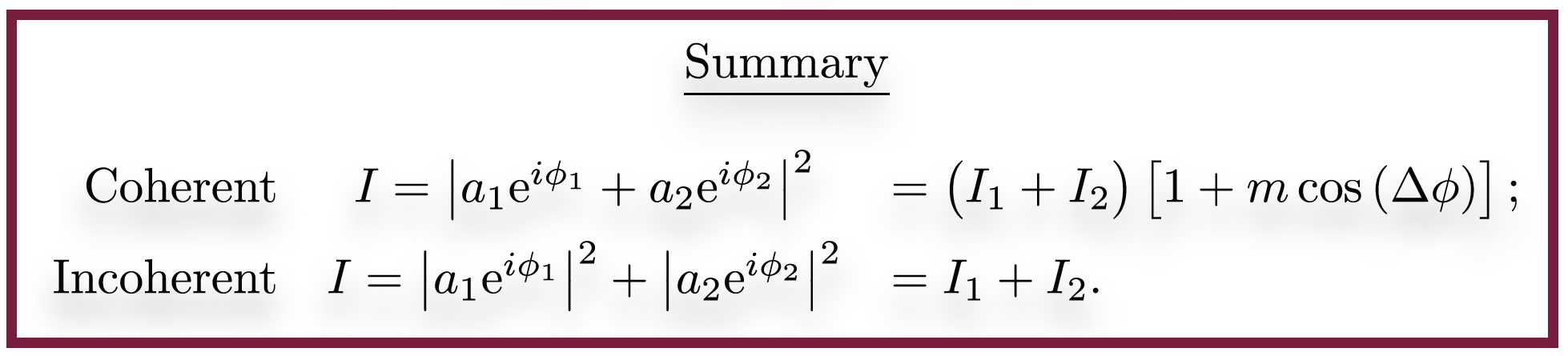
相干成像系统和非相干成像系统

在4f系统里讨论：

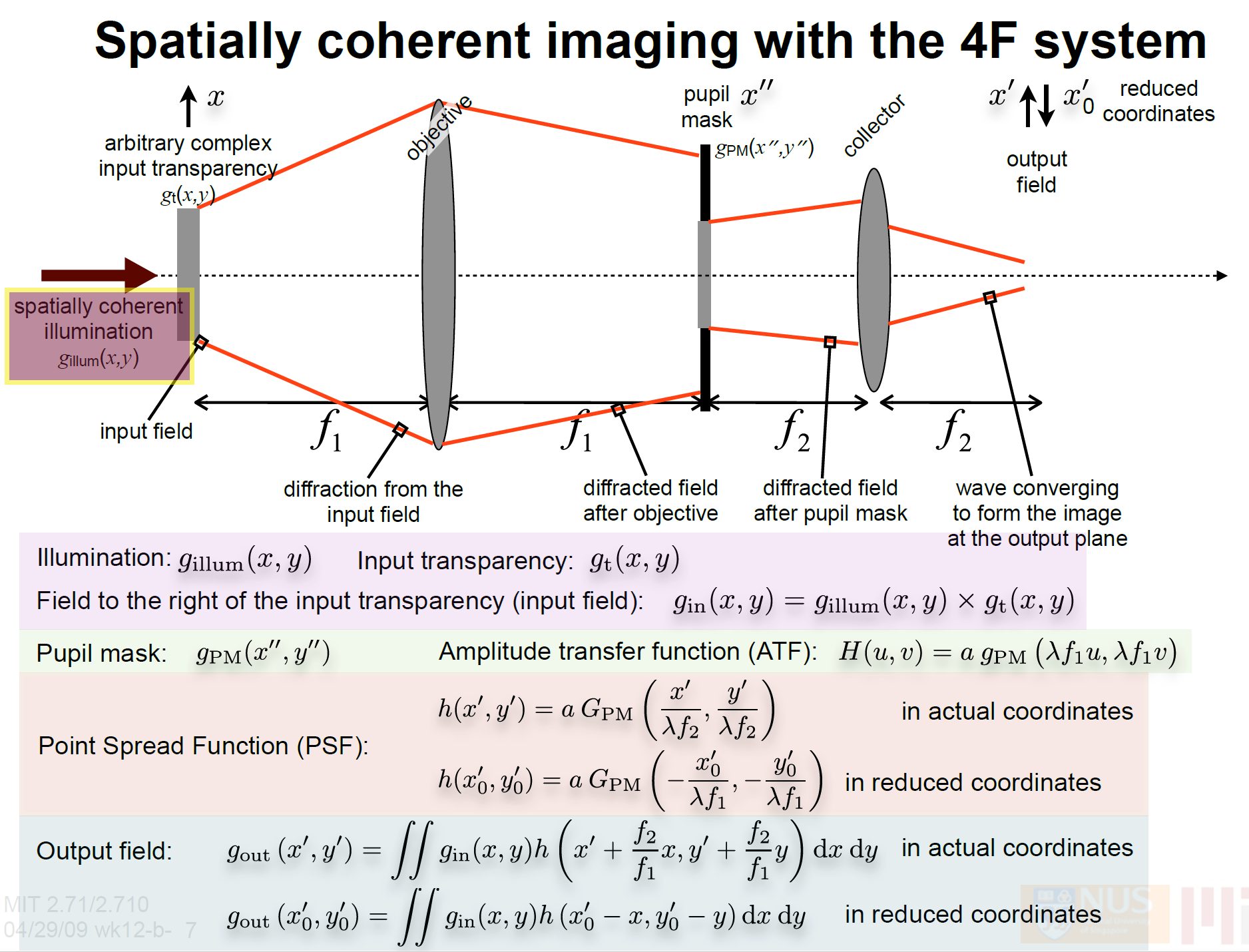
其中reduced coordinates是归一化的坐标系。

相干成像系统：

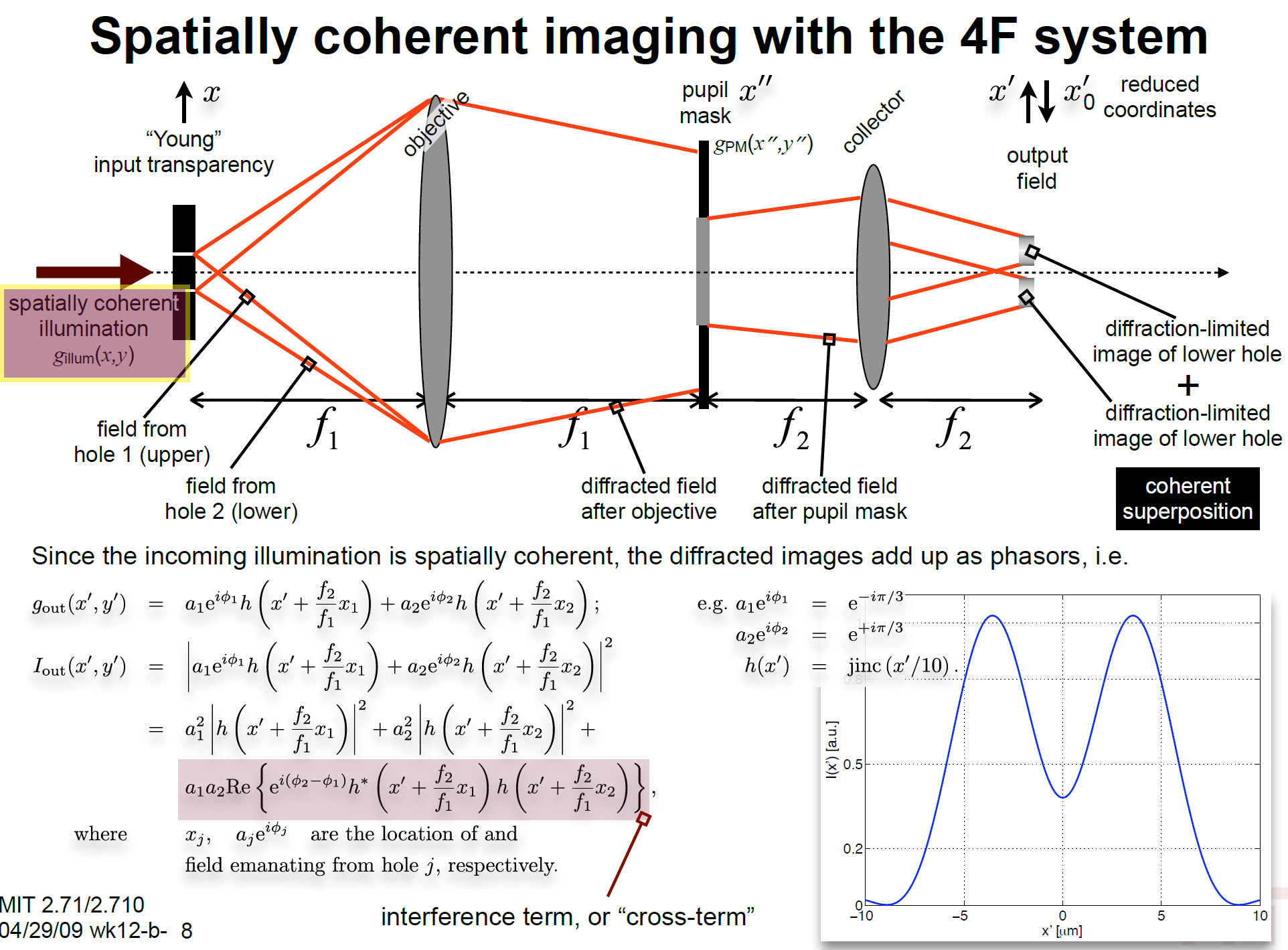
非相干成像系统：

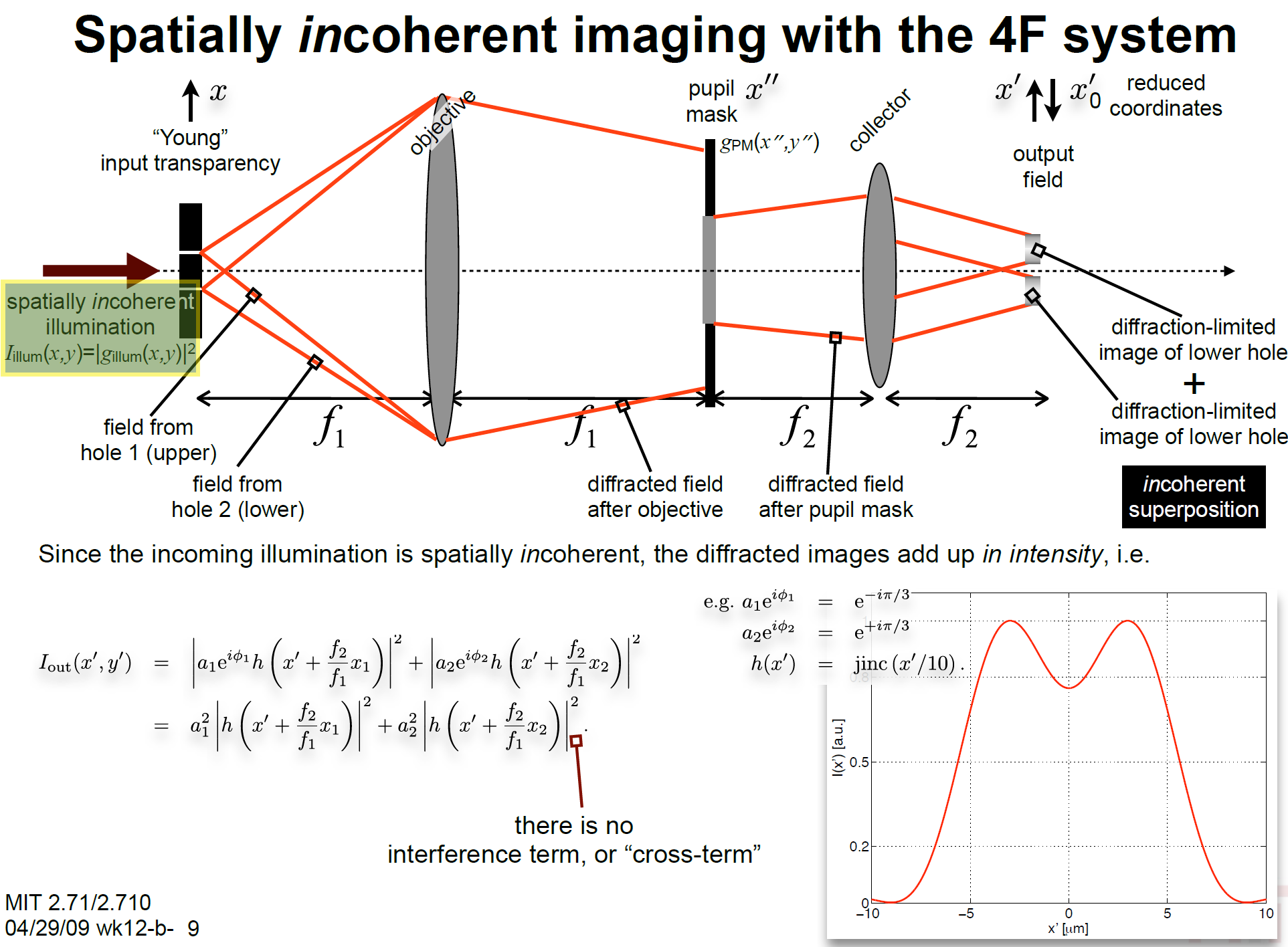
将他们放在一起，并用不同的相位输入，到不同的入瞳函数中。

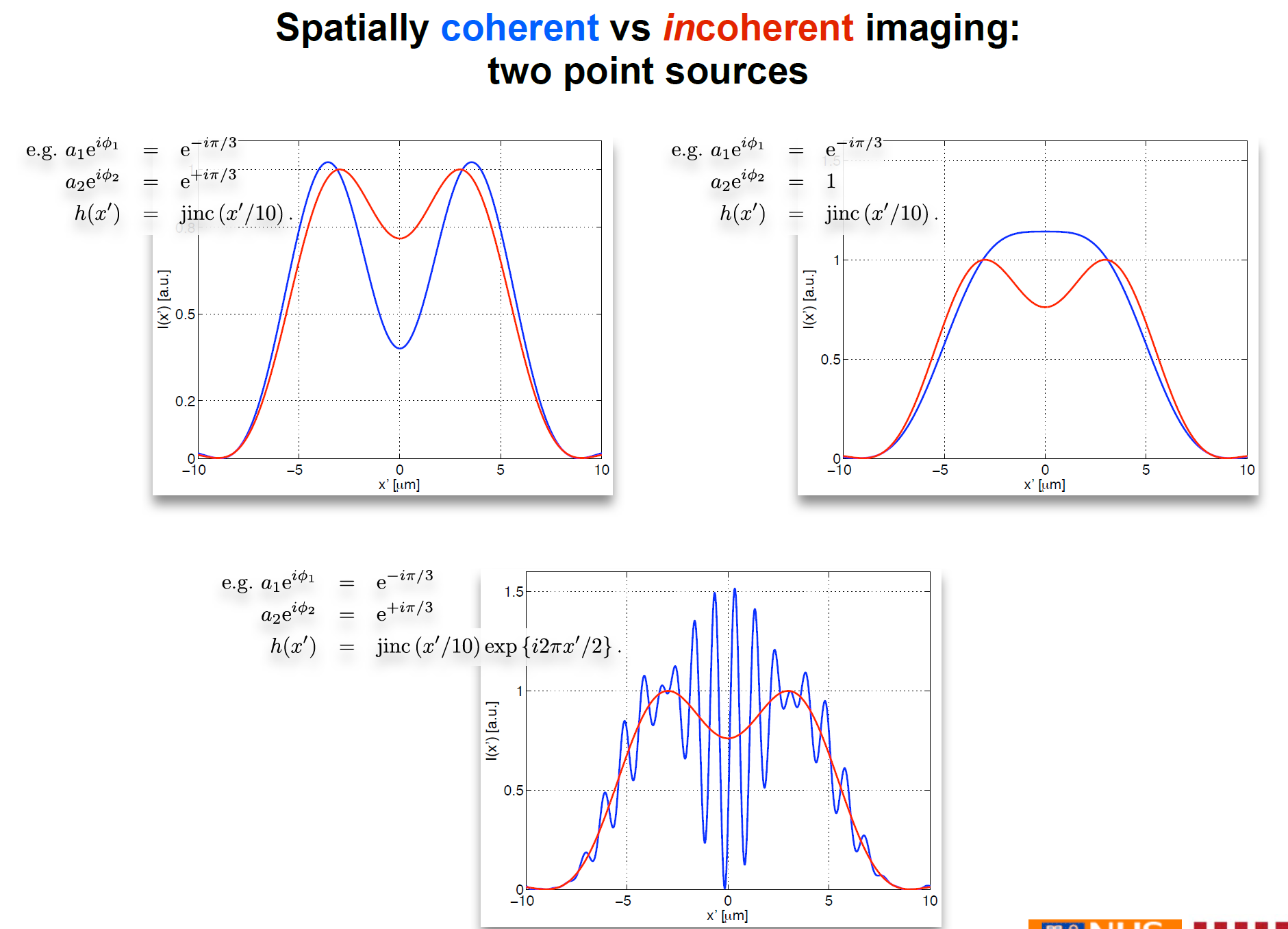
可以看到，非相干成像和相位以及入瞳的相位没有关系，相干成像和相位的关系较大。

相干成像CTF和非相干成像OTC之间的区别

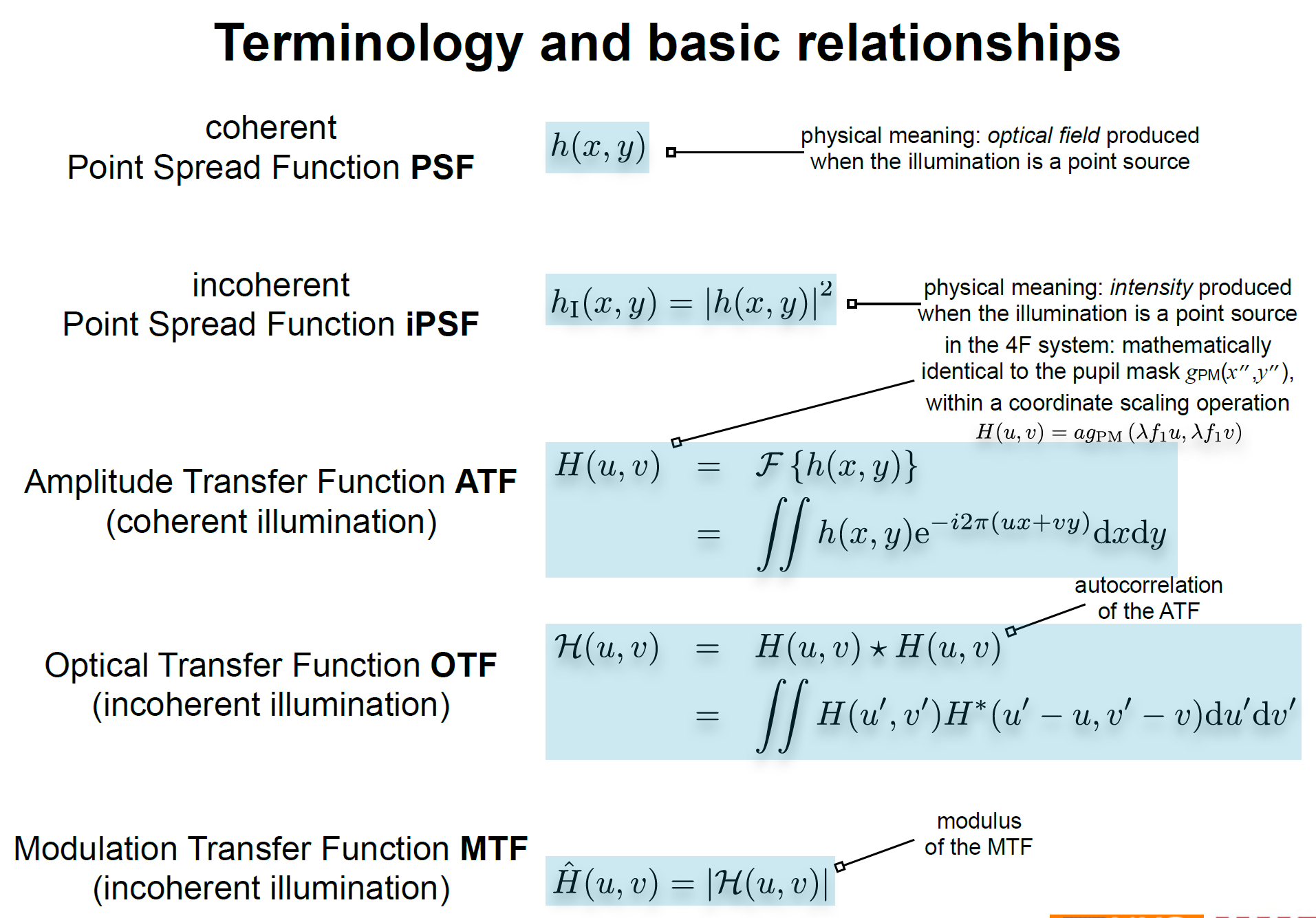
在图中，相干成像的叫做cPSF/PSF，非相干的叫做iPSF。非相干成像系统的iPSF是cPSF（一般是光瞳函数）的强度相乘。

ATF图中是强度传输函数，就是我们平时说的CTF，就是cPSF的傅里叶变换。

OTF是非相干成像才有的概念，是iPSF的傅里叶变换，也是CTF的自相关。MTF就是OTF的强度部分。

利用角谱理论，可以在空域概念（PSF,iPSF），频域概念(CTF/ATF，OTF)之间建立起脉络。

相干成像

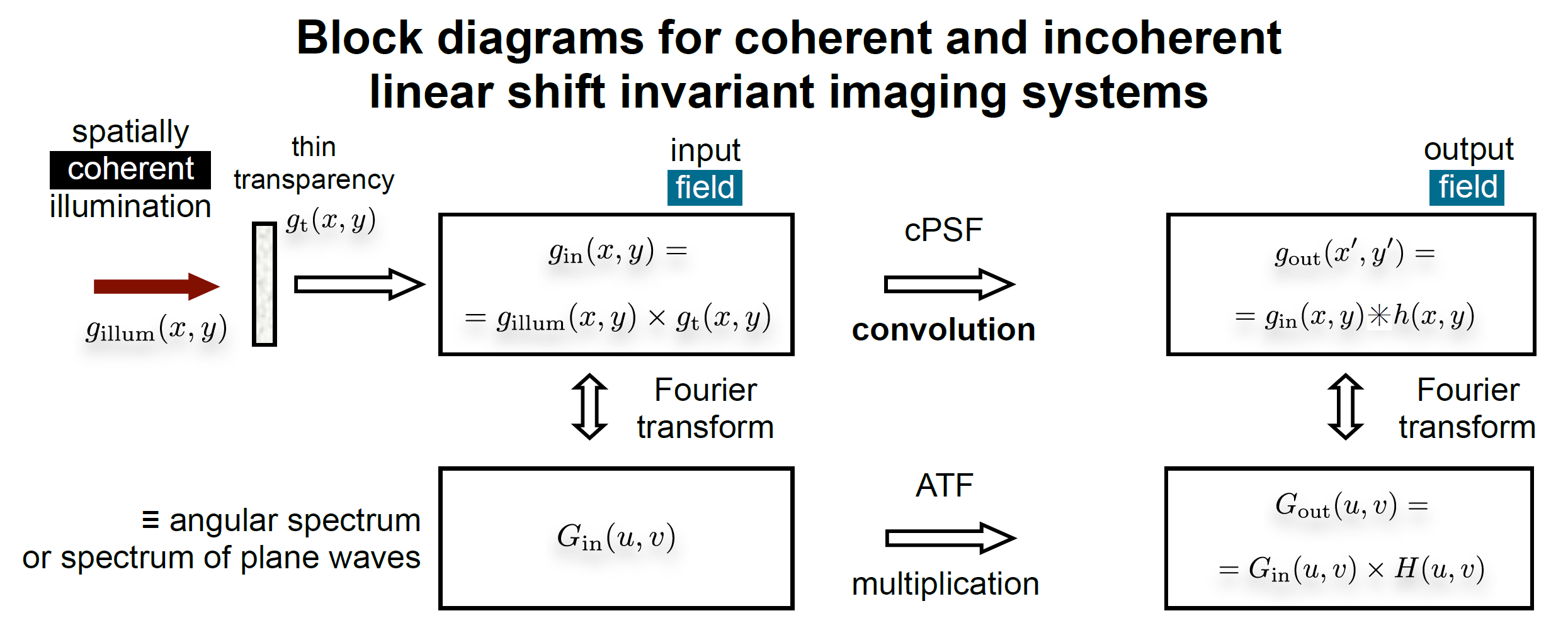
非相干成像

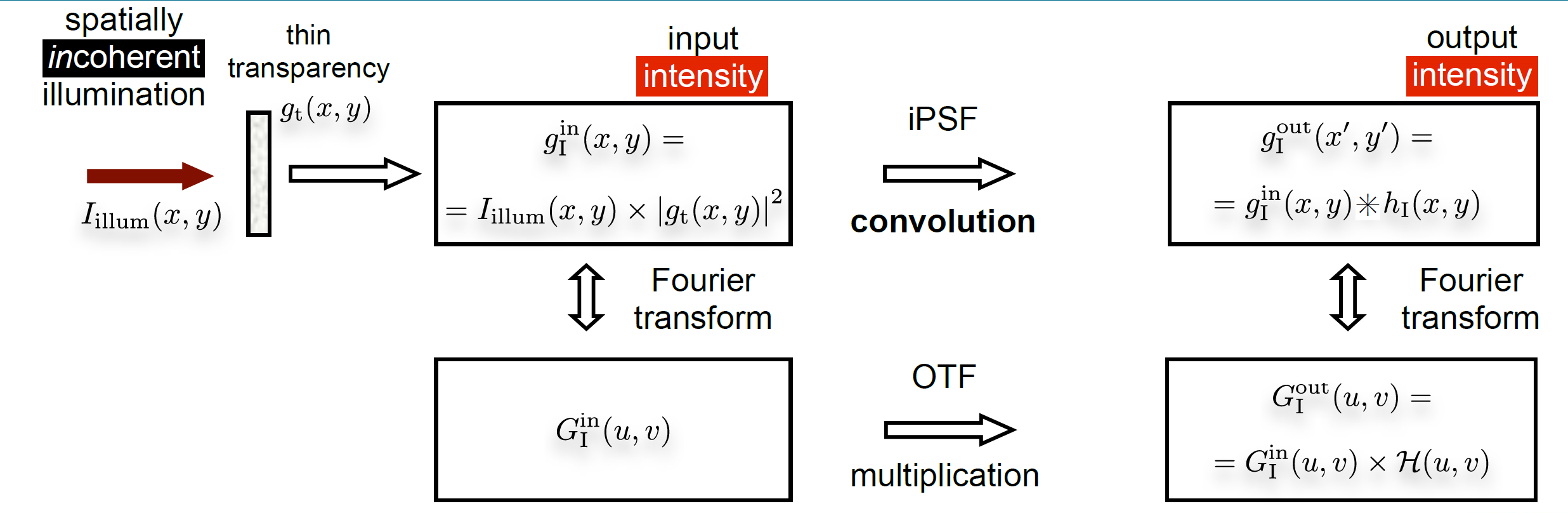
通过推导，我们可以得到MTF其实就是相同空间频率下的强度对比度的表示。

We conclude that the value of the MTF at a given spatial frequency expresses the contrast at that spatial frequency relative to the contrast of the same spatial frequency in the input intensity pattern. The contrast change is the result of propagation through the optical system, including free space diffraction and the effect of the pupil mask.

最后放一个相干成像和非相干成像的效果

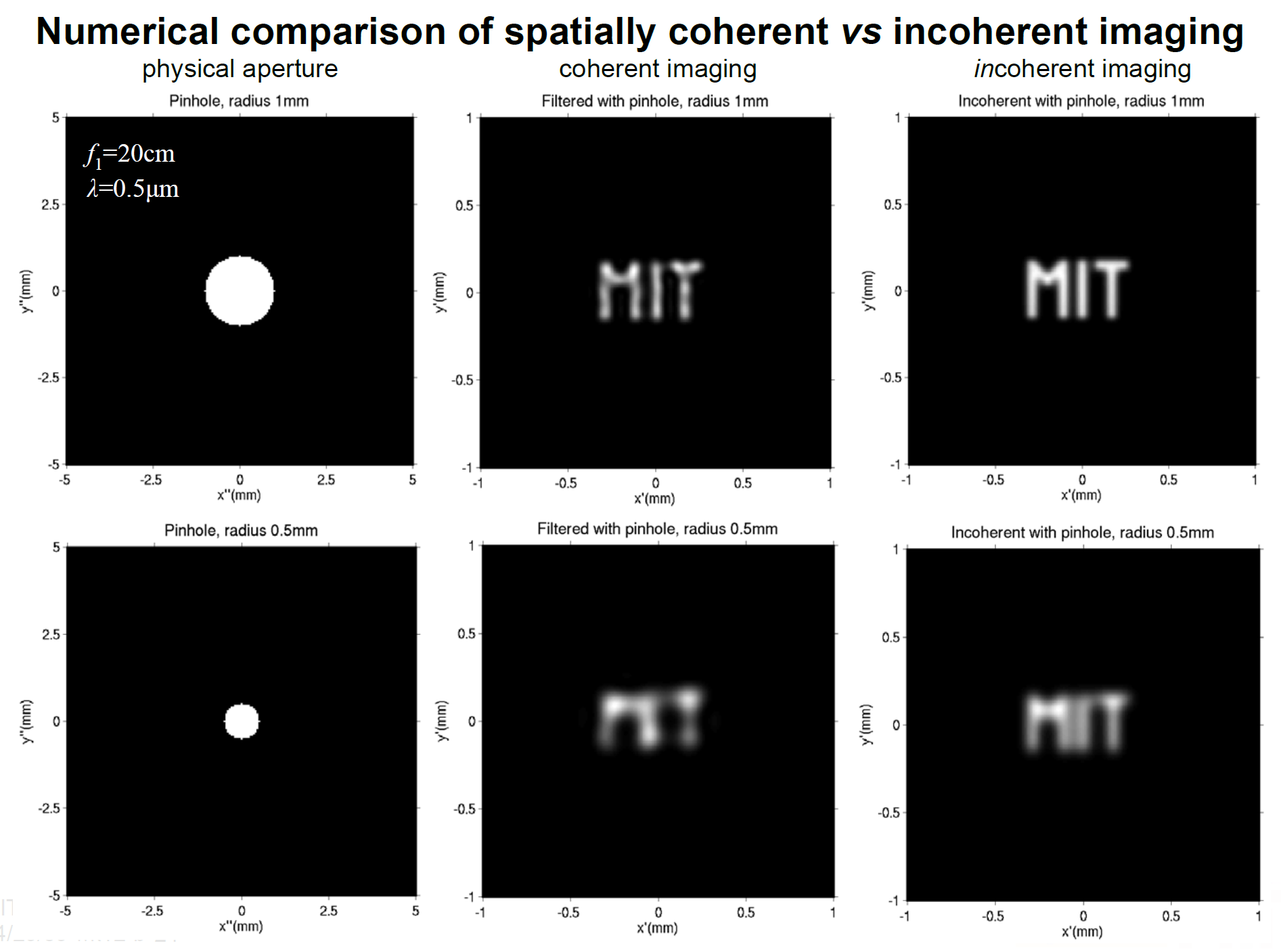
总结：

• Incoherent generally gives better image quality: –no ringing artifacts –no speckle –higher bandwidth (even though higher frequencies are attenuated because of the MTF roll-off) • However, incoherent imaging is insensitive to phase objects • Polychromatic imaging introduces further blurring due to chromatic aberration (dependence of the MTF on wavelength)