[TOC]

光学的分类

根据光学的尺度来进行研究，光学可以分为三类，射线／几何光学(Rays)，物理光学／波动光学（Wave）,电磁波（Electromagnetic waves）。

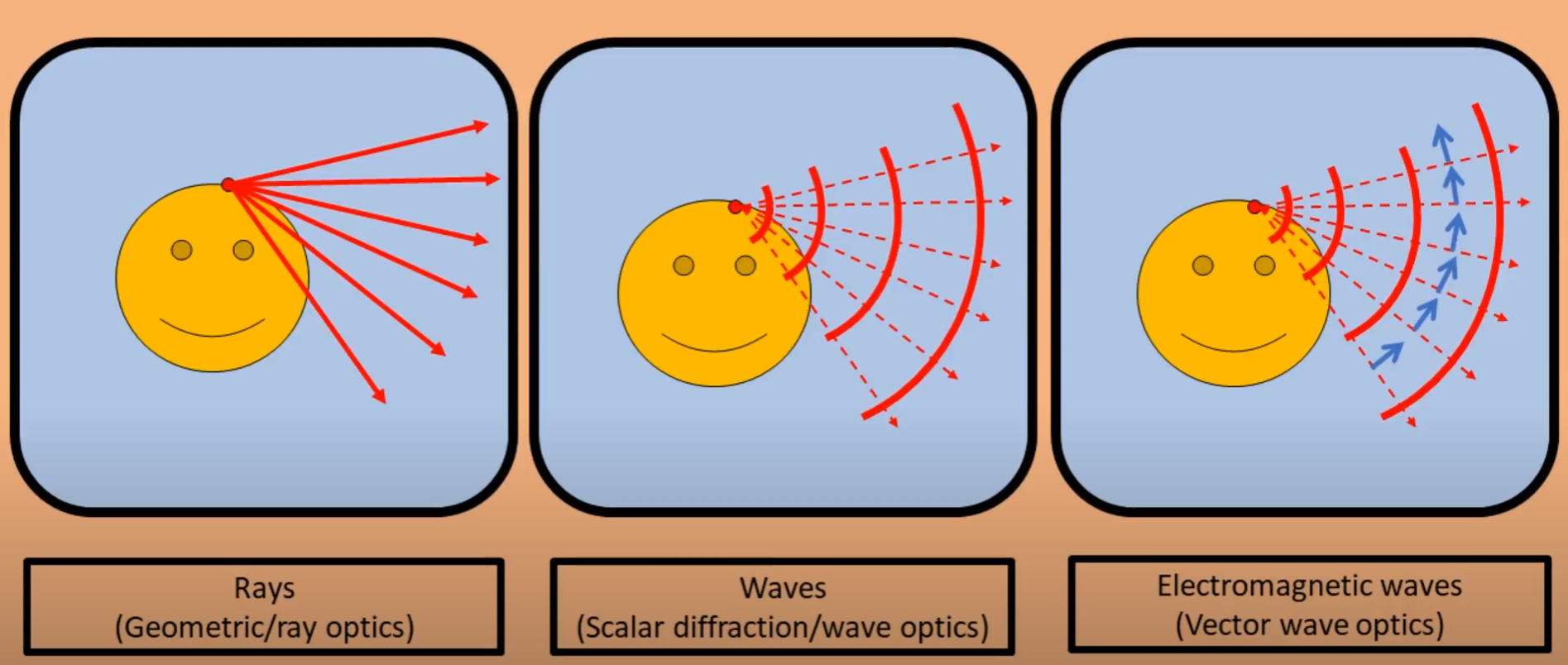
几何光学

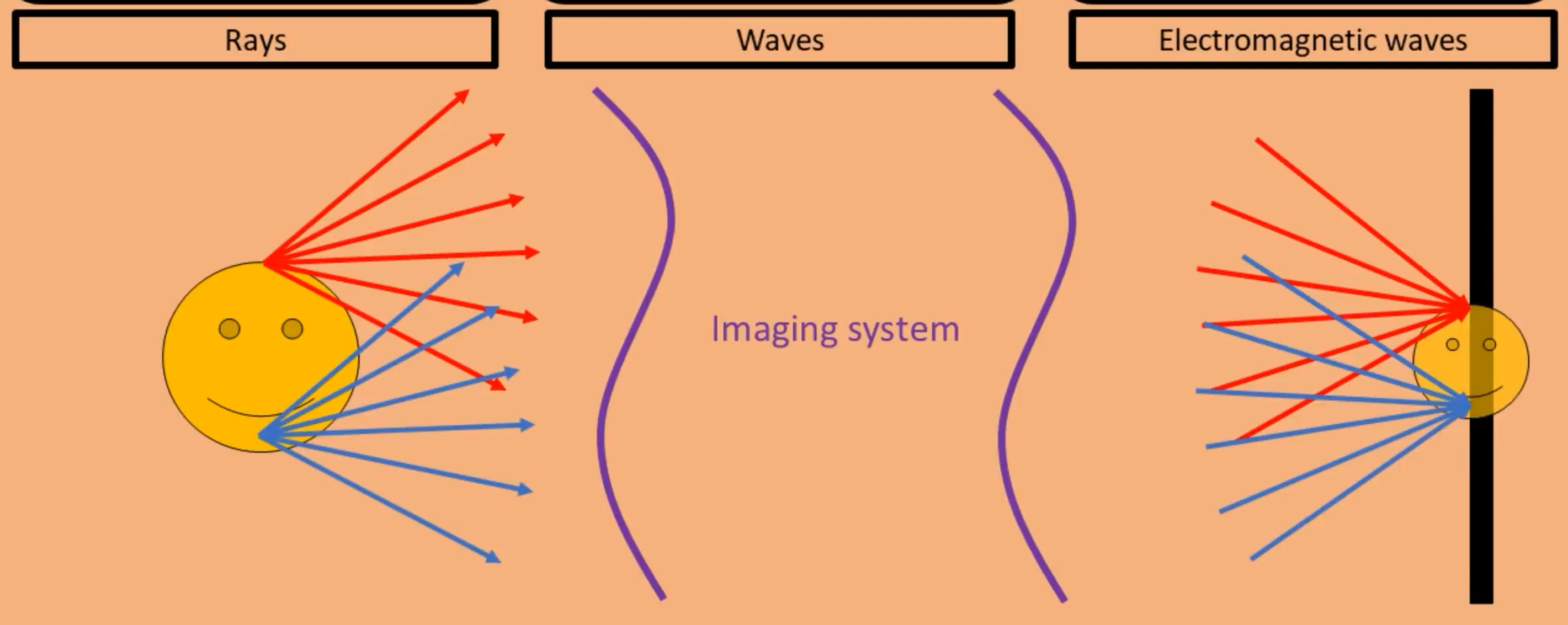
几何光学是把光当作射线一样的直线，通过光学系统，直线道道成像面进行成像。

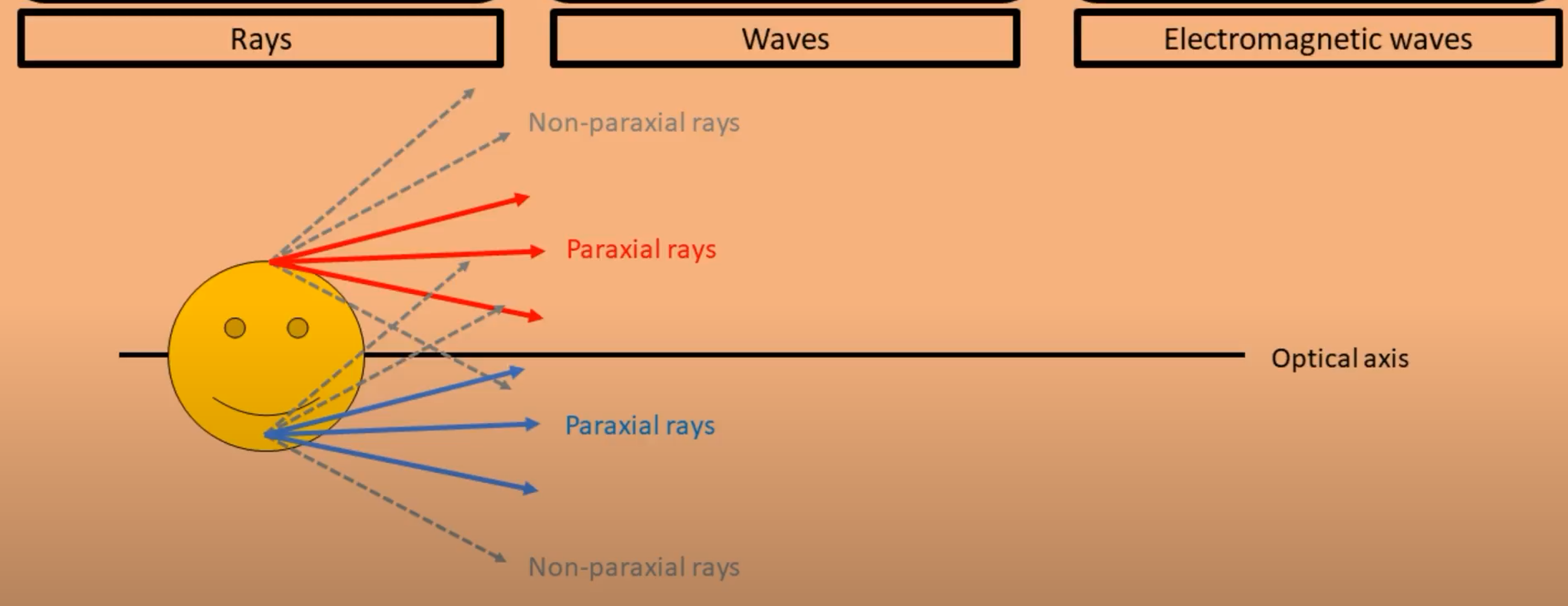
几何光学需要旁轴近似（Paraxial approximation）。在主光线周围的光线是旁轴光线。在光学上称为高斯光学（Gaussian optics）。

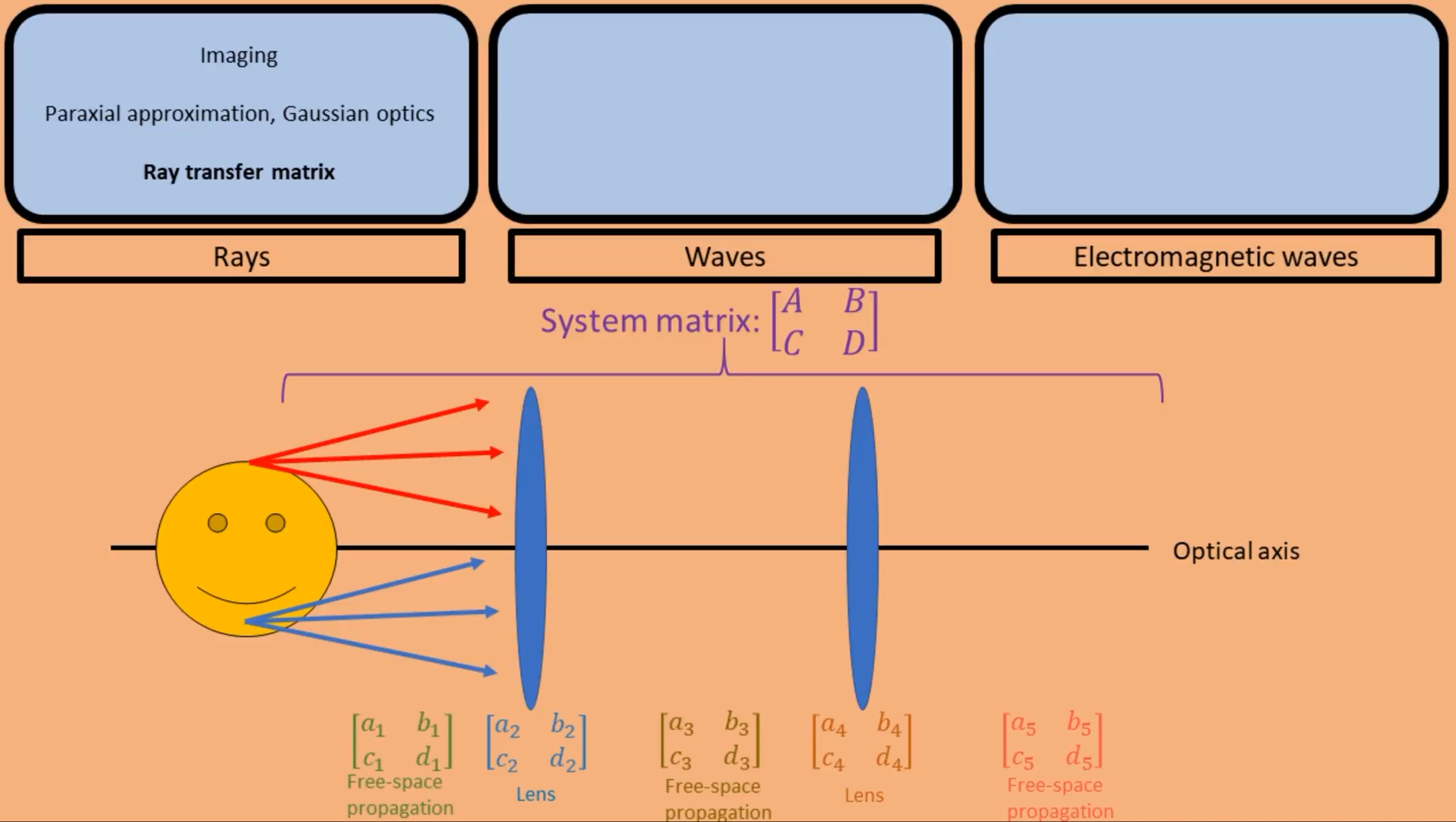
光在自由空间传播和每种光学元件传播，都可以看做是一个矩阵过程。所以几何光学的分析也可以通过射线传输矩阵（Ray transfer matrix）进行分析。

几何光学的缺点：在一些实验条件下，是不符合射线光学的理论。比如双缝实验，同一束激光透过两个缝。如果符合射线光学，在观察面上那应该是两个点。

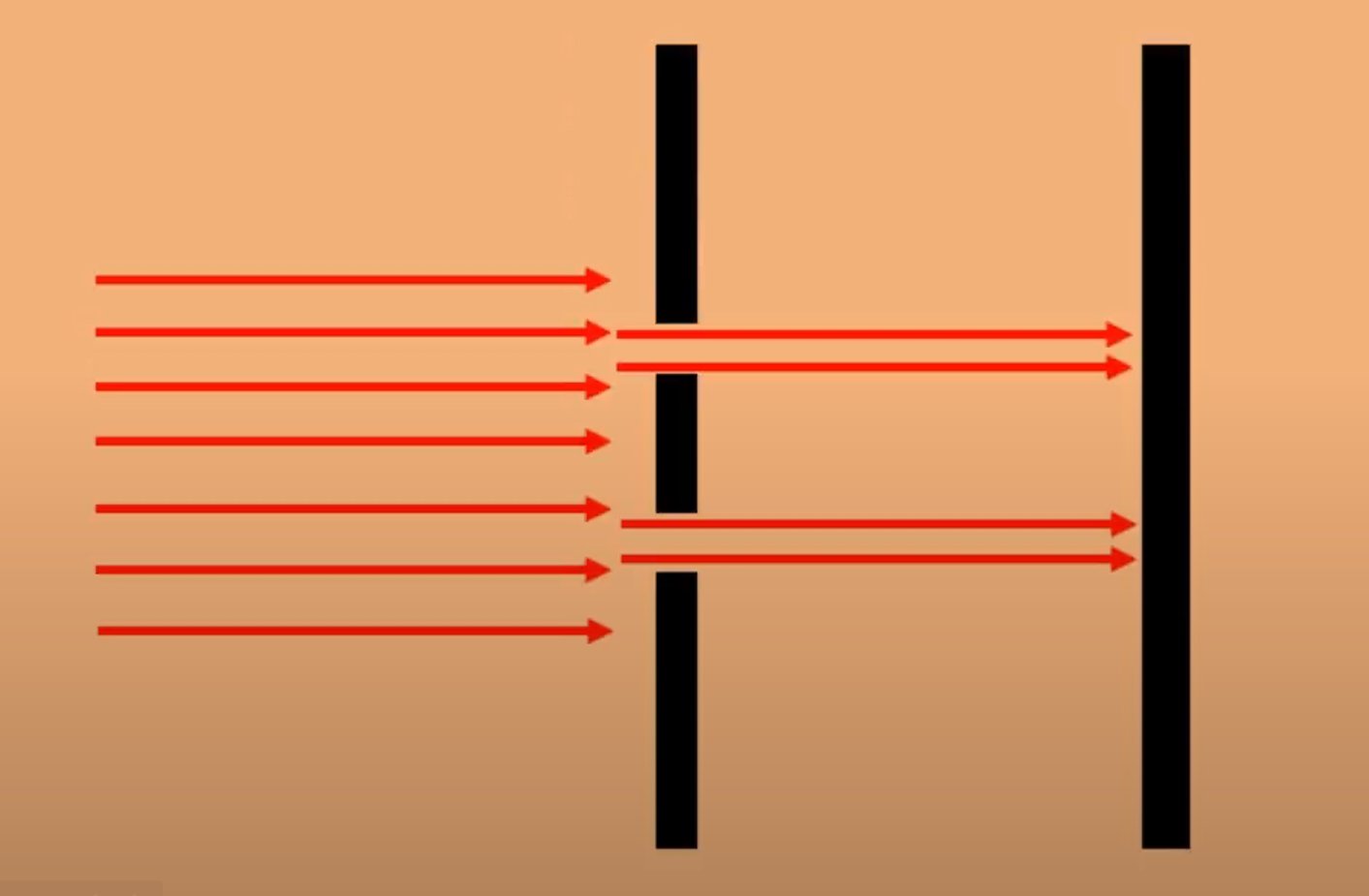
但是实际情况下会存在衍射，两束光就会有干涉现象，在观察面就会有干涉条纹，如下图所示。

我们知道，光束是会有衍射的情况，如下图所示，光透过一个小缝，可以当作一个点光源继续向前传播。

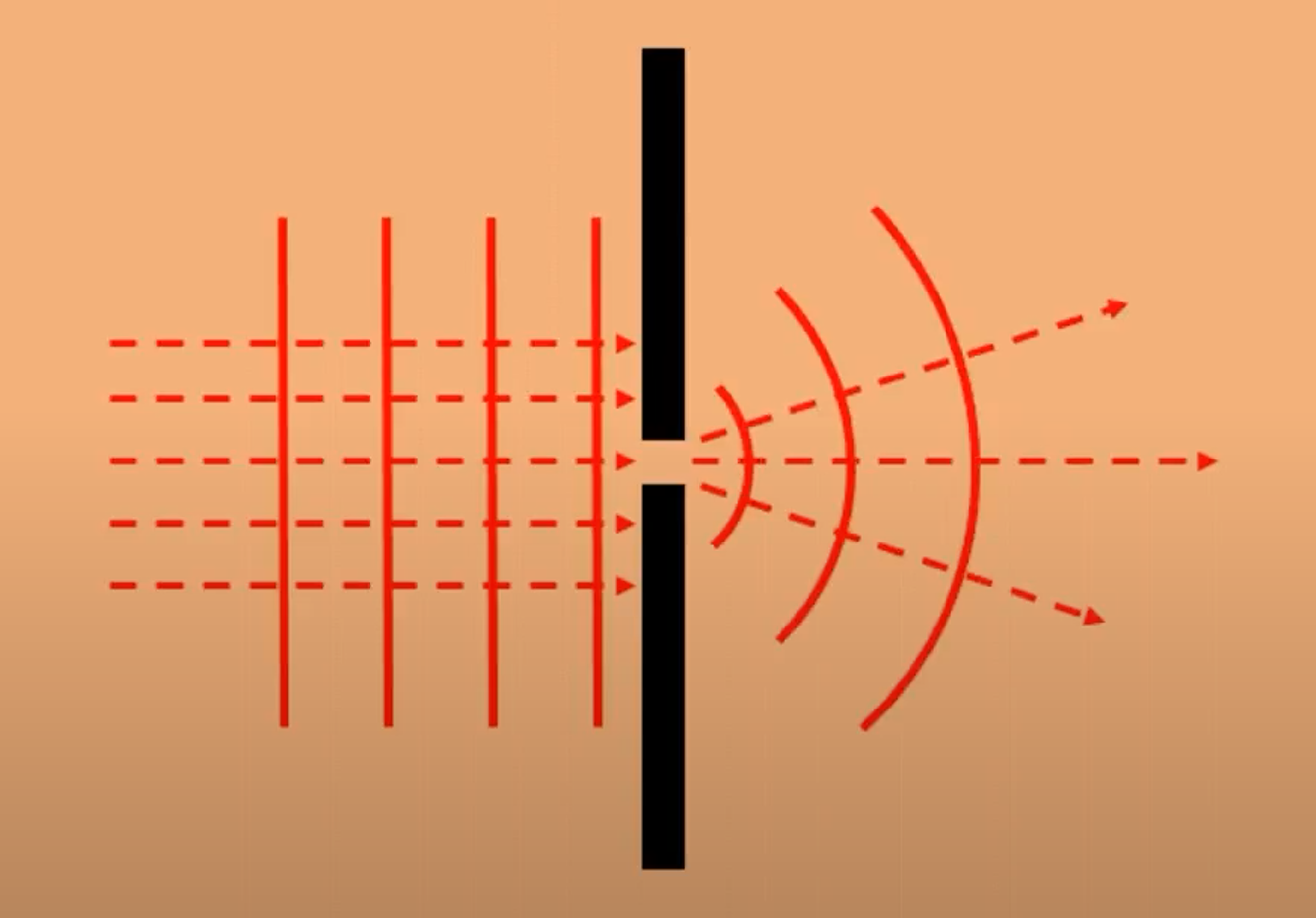
如果要用几何光学来分析，或者说实际情况下符合几何光学的理论，只有在孔径达到一定的大小，才会有近似于几何光学的程度。

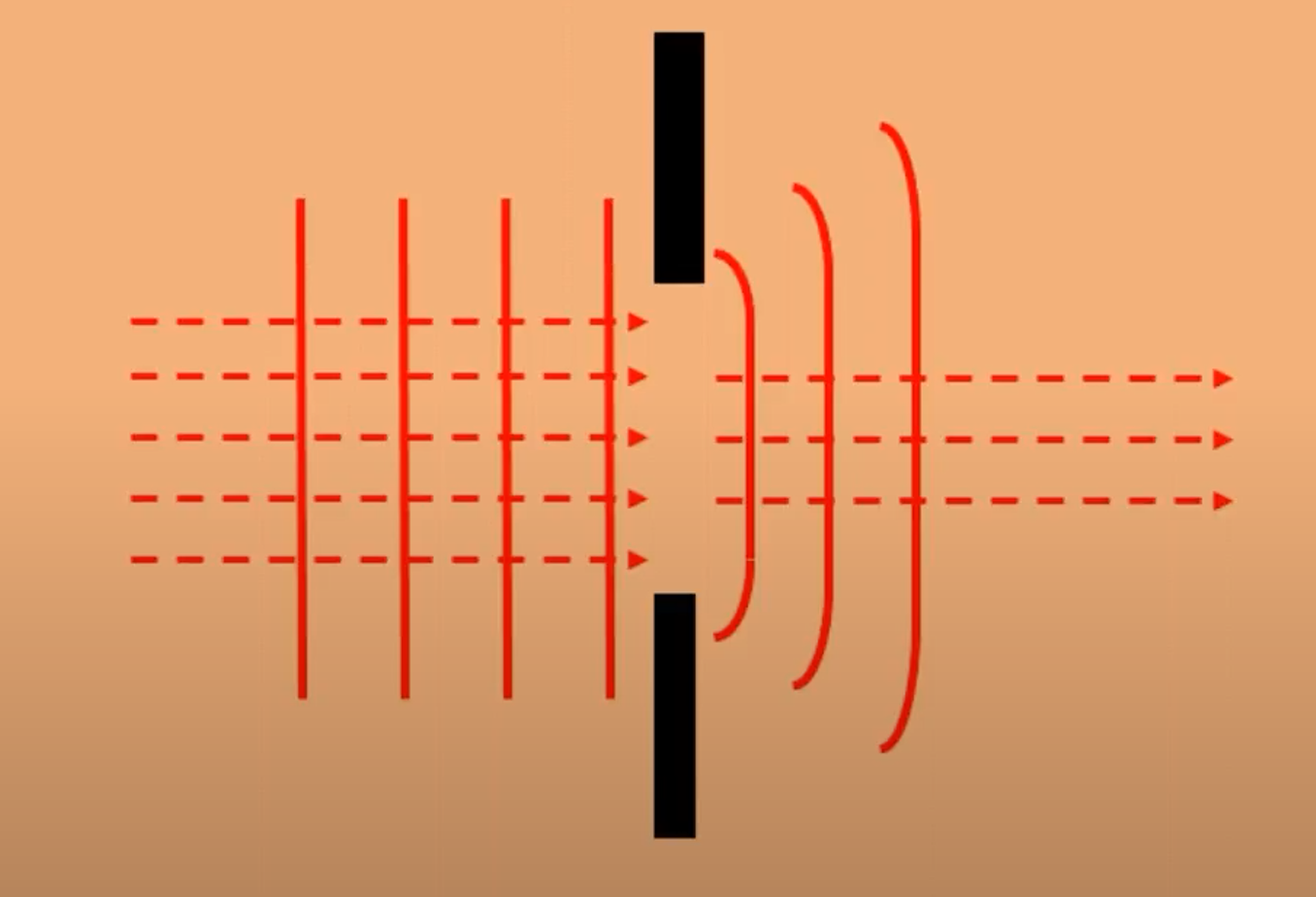
所以，几何光学适用于较大的尺度，在微小尺度下，就要用波动光学（Wave）来分析。

波动光学

波动光学里面我们假设有一个初始面，发射光线。在观察面会得到什么样的结果。通过建立标量衍射方程和亥姆霍兹方程来分析。

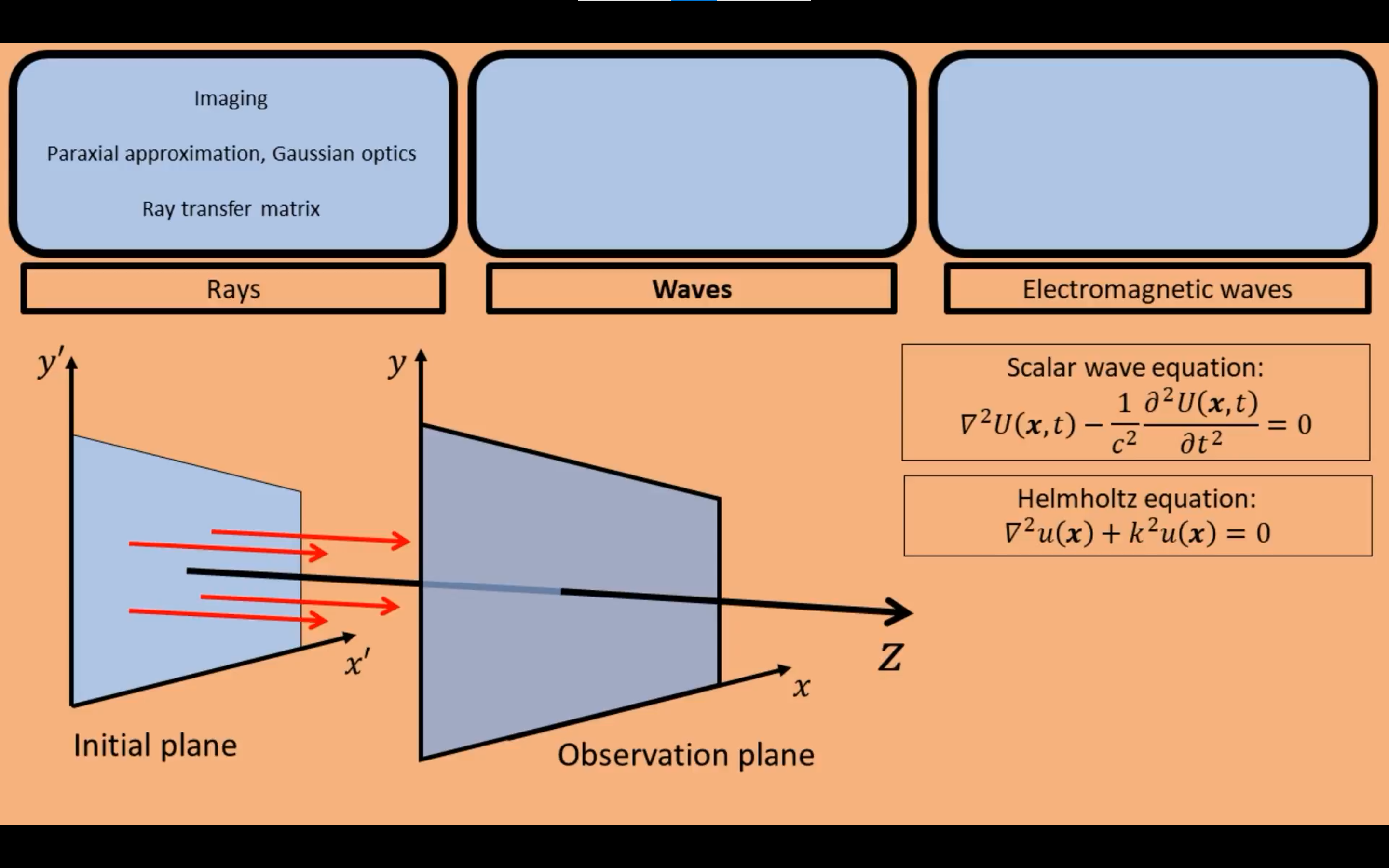
有两种方法分析简化这个方程：

角谱法

角谱发是将初始面的光线分解成很多个不同方向的平面波。将这些平面波传播到观察面。然后将所有的平面波加起来。不过这也会导致一些比波长还微小的细节特征被忽略。

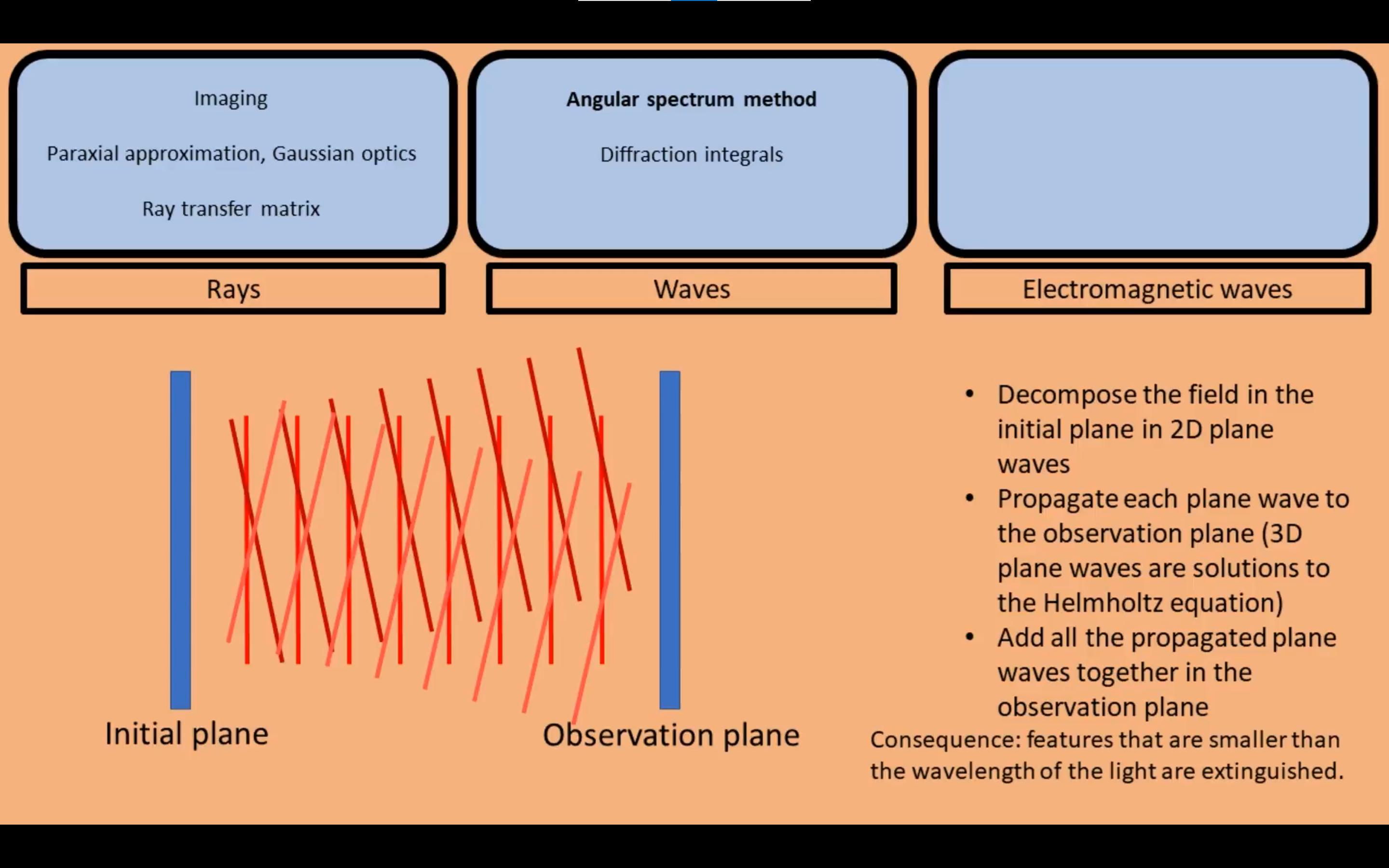
衍射积分方法

衍射积分的方法是将初始面上所有的点都当做球面子波（惠更斯原理+亥姆霍兹方程的格林函数解）；在观测面将所有的点光源加起来。具体的详细解释看后面的博客内容。

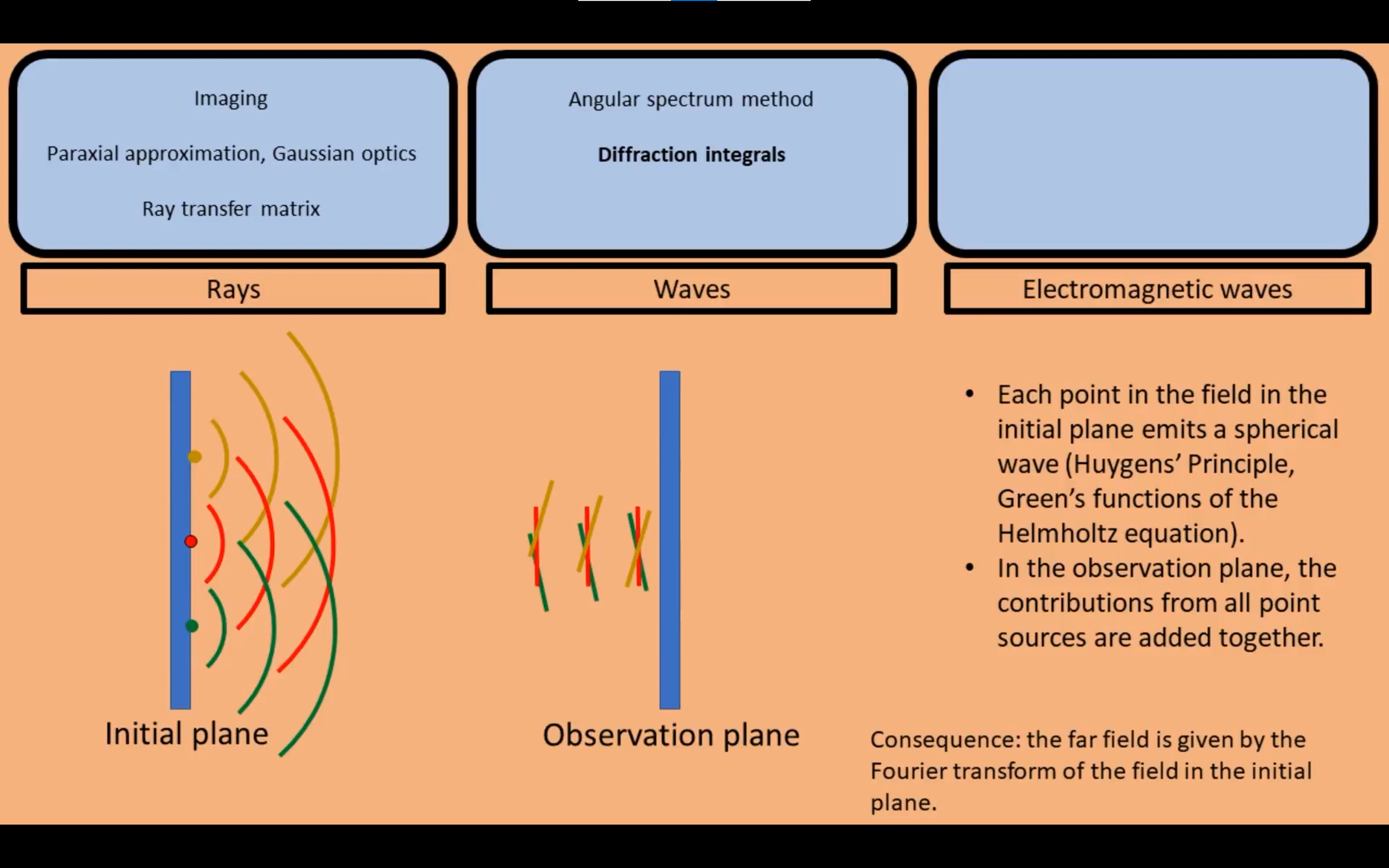
在几何光学上，一个点经过光学系统之后还是一个点。但是对于波动光学，一个点经过光学系统会变成一个有限大小的斑（spot，不知道中文用什么表示好）。

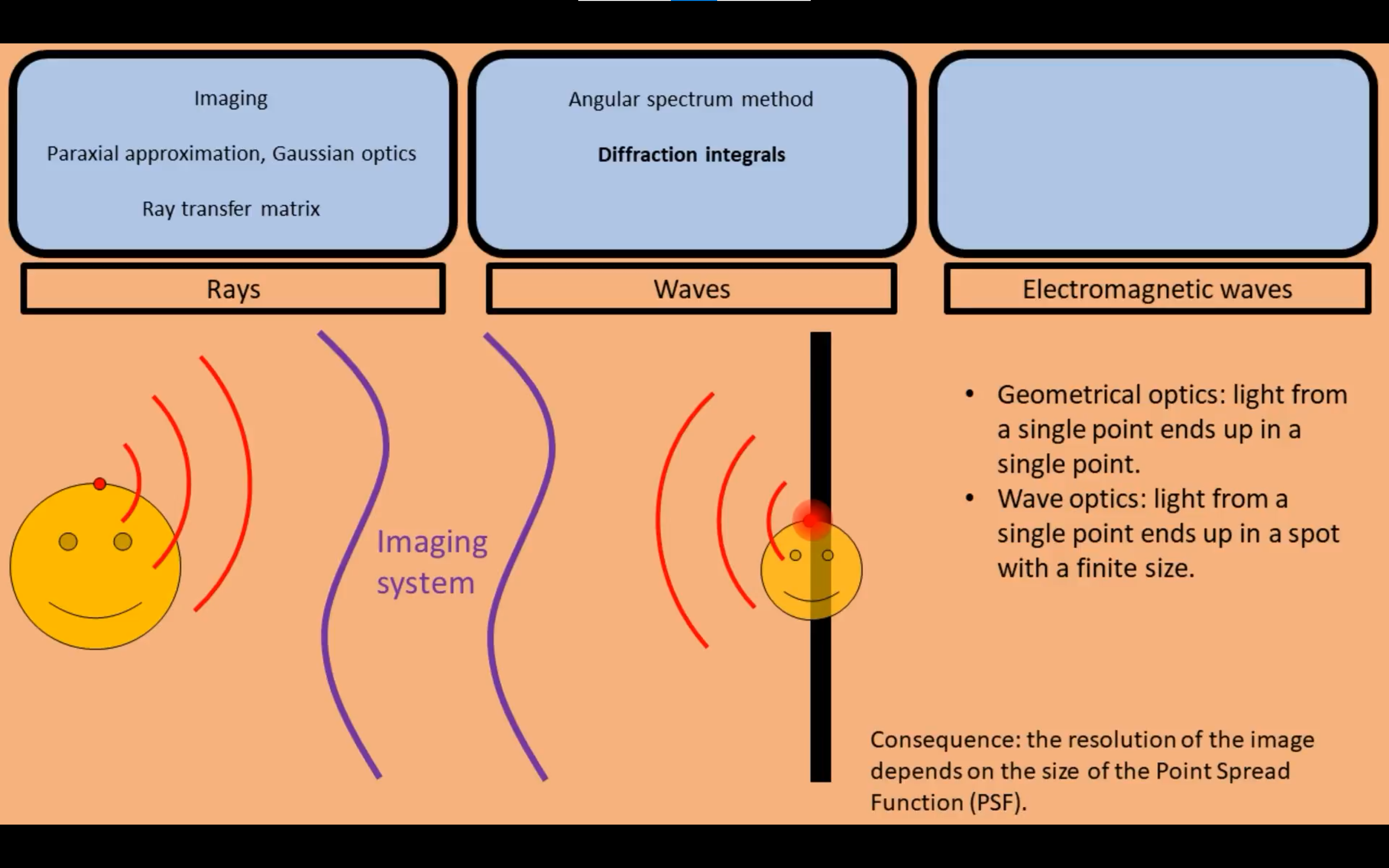
相干性

如下图所示，在激光下可以观察到相干的条纹，但是在太阳光等非相干光的情况下，却观察不到。这就要考虑到光学的相干性

| | | | ———————————————————— | ———————————————————— |

因为在白光情况下，两个孔出射的相位在快速的变化，我们的肉眼只能比较慢的观测。所以最后平均情况下为近似均匀的光。

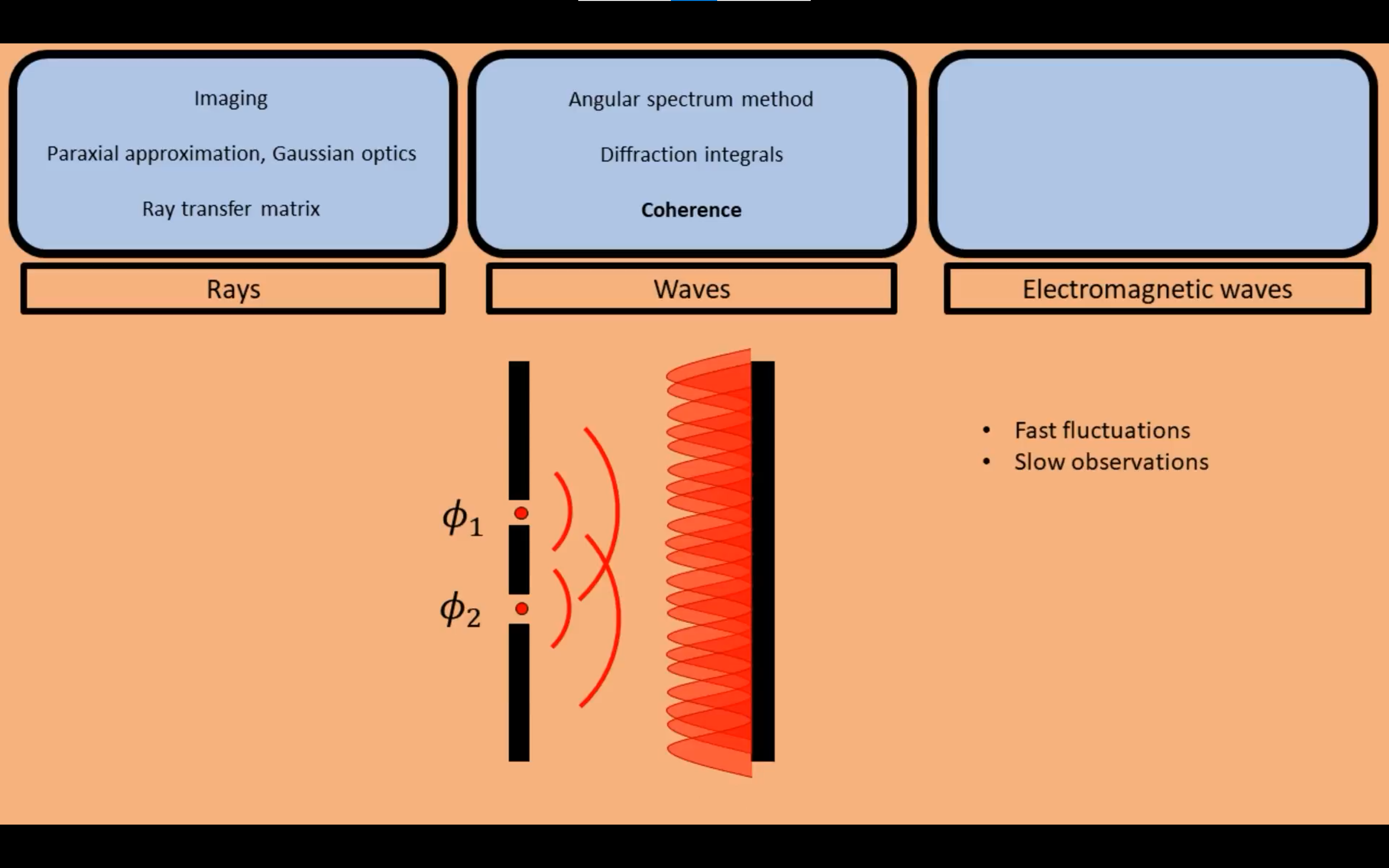
两者相位差越小，相干度越大，则越容易观察到条纹。

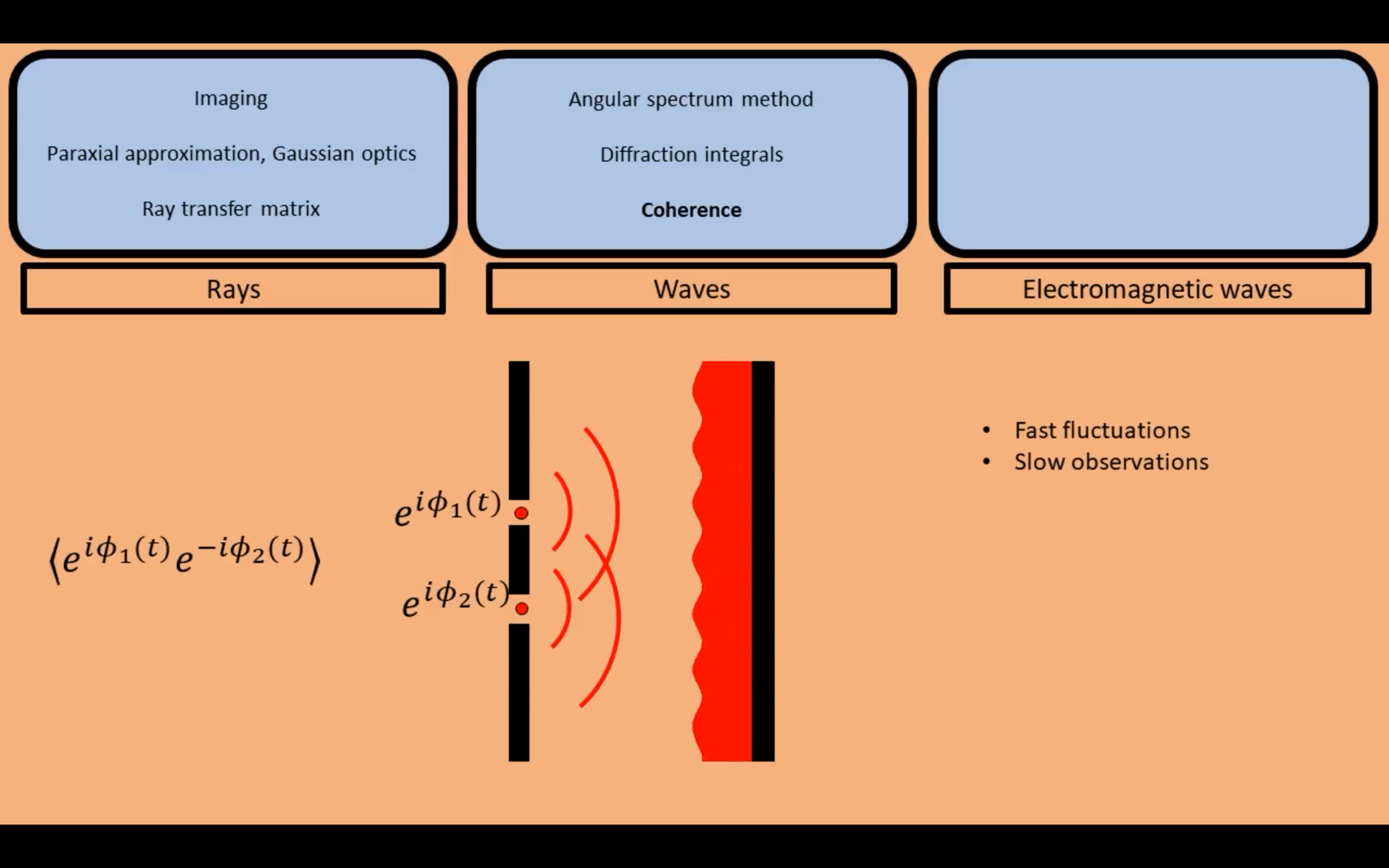
当两者的相位差过于大，则意味着观察不到干涉条纹，两个小孔出射的光没有任何联系，近似是均匀的光。

电磁波

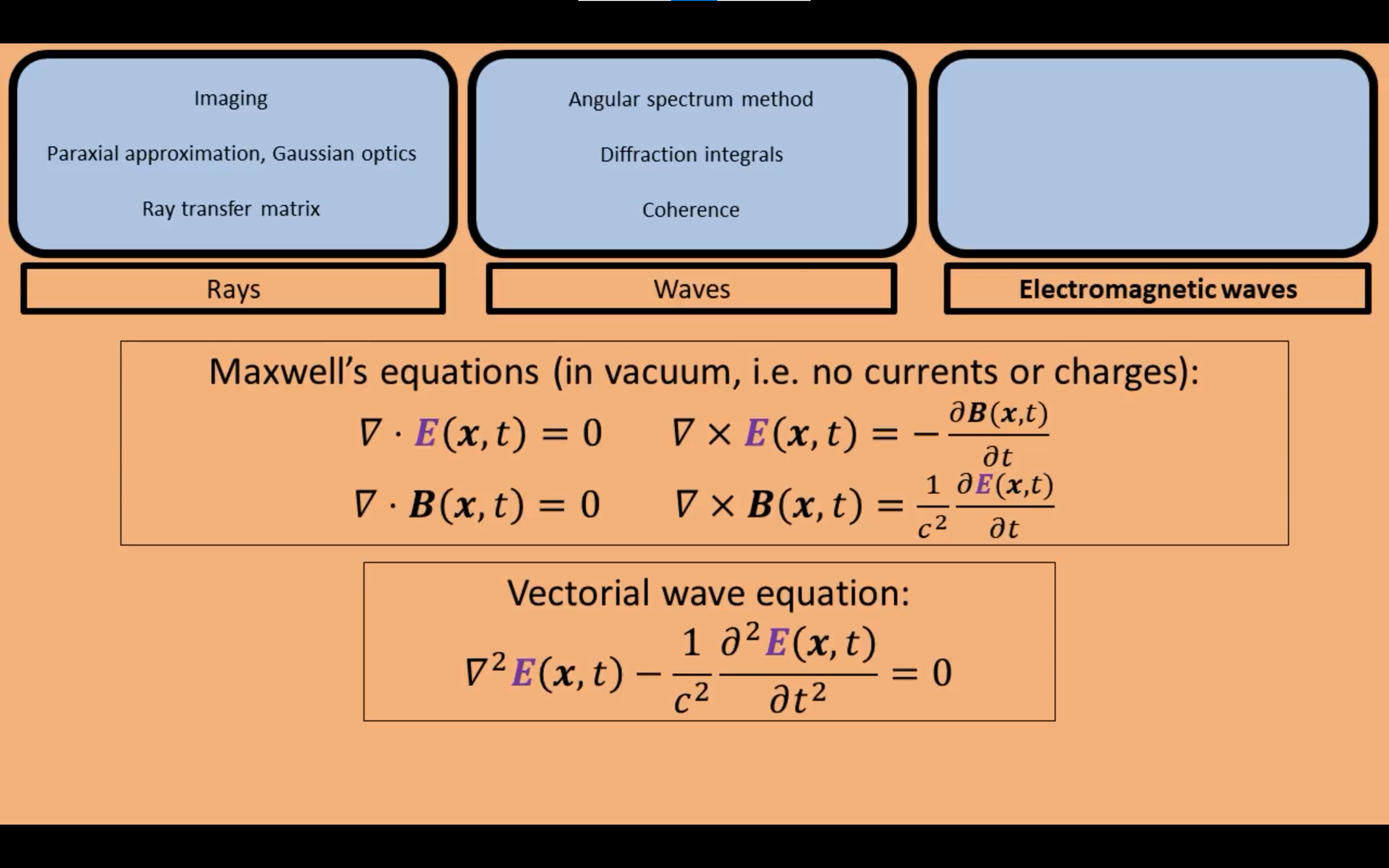
通过解麦克斯韦方程组，以及推导得到向量波动方程。

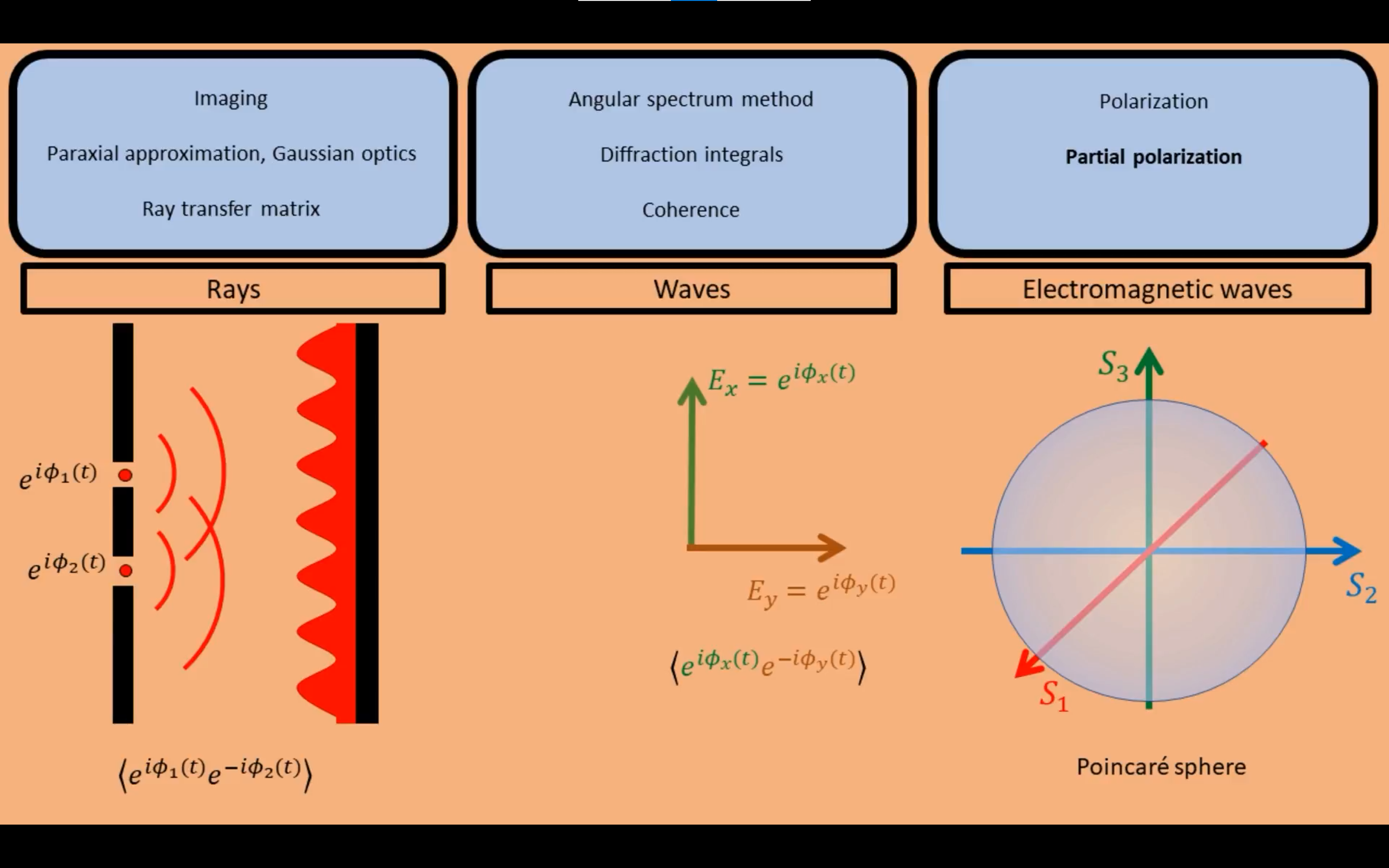
偏振

在电磁学下，因为电场和磁场是有方向的，光有了偏振特性。光的偏振特征和相干性一样，也是两个分量之间的关系。分别是x, y方向上各自的电场分量。这个关系可以用庞加莱球（Poincare sphere）表示。

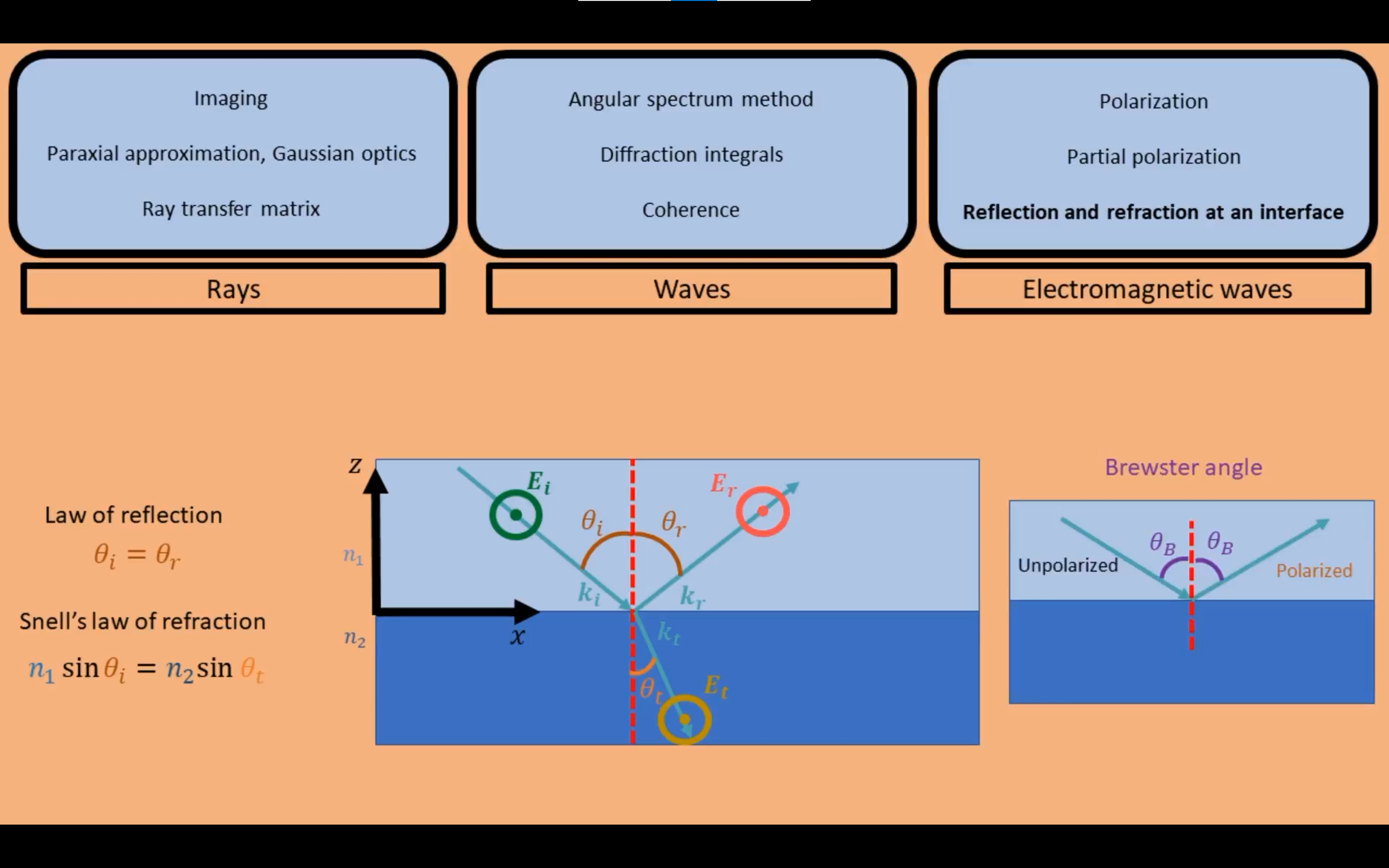
光学的反射，遵从斯涅尔定律。我们可以设计特定的角度，由非偏振光得到偏振光。